
【题目】如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.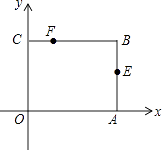
(1)点E的坐标为 , 点F的坐标为;
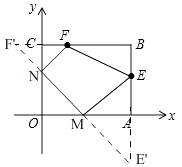
(2)点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
①点E′的坐标为 , 点F′的坐标为;
②求直线E′F′的解析式;
(3)若M为x轴上的动点,N为y轴上的动点,当四边形MNFE的周长最小时,求出点M,N的坐标,并求出周长的最小值.
【答案】
(1)(3,1),(1,2)
(2)(3,﹣1),F'(﹣1,2)
(3)解:如图,∵E(3,1),F(1,2),
∴EF= ![]() ,
,
∵点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
∴连接E'F'和x轴交于M,和y轴交于N,此时四边形MNFE的周长最小,
∴NF=NF',ME=ME',
∵E'(3,﹣1),F'(﹣1,2),
∴E'F'= ![]() =5,
=5,
∴四边形MNFE的周长的最小值为NF+MN+ME+EF
=NF'+MN+ME'+EF=E'F'+EF=5+ ![]() .
.
【解析】解:(1)∵A(3,0),C(0,2),
∴OA=3,OC=2,
∵四边形OABC是矩形,
∴BC∥OA,OC∥AB,BC=OA=3,AB=OC=2,
∴B(3,2),
∵点E是AB的中点,
∴AE= ![]() AB=1,
AB=1,
∴E(3,1),
∵点F在BC上,且CF=1,
∴F(1,2),
所以答案是:(3,1),(1,2),
⑵①由(1)知,E(3,1),F(1,2),
∵点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
∴E'(3,﹣1),F'(﹣1,2),
所以答案是:(3,﹣1),F'(﹣1,2);
②设直线E'F'的解析式为y=kx+b,
∴ ![]() ,
,
∴ 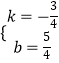 ,
,
∴直线E'F'的解析式为y=﹣ ![]() x+
x+ ![]() ;
;


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】根据下列表中的对应值:
x | 2.1 | 2.2 | 2.3 | 2.4 |
ax2+bx+c | ﹣1.39 | ﹣0.76 | ﹣0.11 | 0.56 |
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
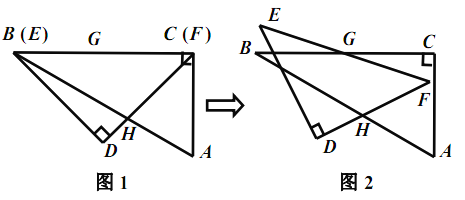
【题目】一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 叠合在一起,边
叠合在一起,边![]() 与
与![]() 重合,
重合,![]() (如图1),点
(如图1),点![]() 为边
为边![]()
![]() 的中点,边
的中点,边![]() 与
与![]() 相交于点
相交于点![]() ,此时线段
,此时线段![]() 的长是 .现将三角板
的长是 .现将三角板![]() 绕点
绕点![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在![]() 从
从![]() 到
到![]() 的变化过程中,点
的变化过程中,点![]() 相应移动的路径长共为 .(结果保留根号)
相应移动的路径长共为 .(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,四边形![]() 各顶点的坐标分别为
各顶点的坐标分别为![]() ,动点
,动点![]() 与
与![]() 同时从
同时从![]() 点出发,运动时间为
点出发,运动时间为![]() 秒,点
秒,点![]() 沿
沿![]() 方向以
方向以![]() 单位长度/秒的速度向点
单位长度/秒的速度向点![]() 运动,点
运动,点![]() 沿折线
沿折线![]() 运动,在
运动,在![]() 上运动的速度分别为
上运动的速度分别为![]() (单位长度/秒).当
(单位长度/秒).当![]() 中的一点到达
中的一点到达![]() 点时,两点同时停止运动.
点时,两点同时停止运动.
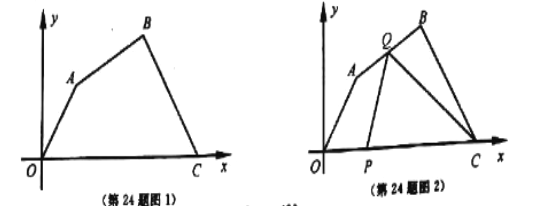
(1)求![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)如图2,当点![]() 在
在![]() 上运动时,求
上运动时,求![]() 的面积
的面积![]() 关于
关于![]() 的函数表达式及
的函数表达式及![]() 的最大值;
的最大值;
(3)在![]() ,
,![]() 的运动过程中,若线段
的运动过程中,若线段![]() 的垂直平分线经过四边形
的垂直平分线经过四边形![]() 的顶点,求相应的
的顶点,求相应的![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com