
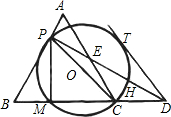
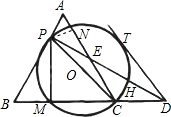
 运动至点A,B),以PC为直径作⊙O交BC于M,连接PD,交⊙O于H,交AC于E,连接PM.
运动至点A,B),以PC为直径作⊙O交BC于M,连接PD,交⊙O于H,交AC于E,连接PM.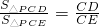 .
.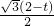 ,
, ×CD×PM=
×CD×PM=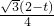 (0<t<2).
(0<t<2). (2-t),MC=2-BM=
(2-t),MC=2-BM= (2+t),MD=MC+1=2+
(2+t),MD=MC+1=2+ t;
t; t,
t,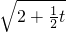 .
.
 PM•CD,S△PCE=
PM•CD,S△PCE= PN•CE,
PN•CE,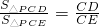 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com