
【题目】已知正方形ABCD中,点E、F分别为边AB、BC上的点,连接CE、DF相交于点G,CE=DF.
(1)如图①,求证:DF⊥CE;
(2)如图②,连接BD,取BD的中点O,连接OE、OF、EF,求证:△OEF为等腰直角三角形
(3)如图③,在(2)的条件下,将△CBE和△DCF分别沿CB、DC翻折到△CBM和△DCN的位置,连接OM、ON、MN,若AE=2BE,ON=![]() ,求EG的长.
,求EG的长.

【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)如图1中,证明Rt△CBE≌△Rt△DCF(HL),即可解决问题.
(2)如图2中,连接OC.想办法证明△OBE≌△OCF(SAS),即可解决问题.
(3)如图3中,连接OC.设BE=a,则BM=EB=CF=CN=a,AE=2a,BC=AB=3a,首先证明△OMN是等腰直角三角形,利用勾股定理求出a即可解决问题.
(1)如图1中,

∵四边形ABCD是正方形,
∴BC=CD,∠B=∠DCF=90°,
∵DE=CE,
∴Rt△CBE≌△Rt△DCF(HL),
∴BE=CF,∠ECB=∠CDF,
∵∠ECB+∠DCE=90°,
∴∠CDF+∠DCE=90°,
∴∠CGD=90°,
∴EC⊥DF.
(2)如图2中,连接OC.
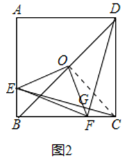
∵CB=CD,∠BCD=90°,OB=OD,
∴OC=OB=OD,OC⊥BD,
∴∠OCB=45°,
∵四边形ABCD是正方形,
∴∠ABD=45°,
∴∠OBE=∠OCF,
∵BE=CF,OB=OC,
∴△OBE≌△OCF(SAS),
∴OE=OF,∠BOE=∠COF,
∴∠EOF=∠BOC=90°,
∴△EOF是等腰直角三角形.
(3)如图3中,连接OC.设BE=a,则BM=EB=CF=CN=a,AE=2a,BC=AB=3a,

∵BE=BM,CF=CN,BE=CF,
∴BM=CN,
∵OB=OC,∠OBM=∠OCN=135°,BM=CN,
∴△OBM≌△OCN(SAS),
∴∠BOM=∠COM,
∴∠MON=∠BOC=90°,
∴△MON是等腰直角三角形,
∵OM=ON=![]() ,
,
∴MN=2![]() ,
,
在Rt△MBN中,a2+16a2=68,
∴a=2(负根已经舍弃),
BE=2,BC=6,EC=2![]() ,
,
∵△CGF∽△CBE,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】小明和妈妈购物后回家,在一楼电梯口看到电梯正显示在顶楼(9楼),他们等了18s后,电梯显示在7楼,这时小明选择走楼梯,高度上升的速度为![]() ,他妈妈则继续等电梯,结果两个人同时到达家所在的楼层。图中所示的细线、粗线分别表示电梯匀速升降、小明走楼梯与一楼地面的距离h(m)与时间t(s)之间的关系。(温馨提示:小明家所在的电梯楼房为3m一层,人们进出电梯所用时间忽略不计,楼层与楼高的关系).
,他妈妈则继续等电梯,结果两个人同时到达家所在的楼层。图中所示的细线、粗线分别表示电梯匀速升降、小明走楼梯与一楼地面的距离h(m)与时间t(s)之间的关系。(温馨提示:小明家所在的电梯楼房为3m一层,人们进出电梯所用时间忽略不计,楼层与楼高的关系).

(1)写出A,B两点的坐标;
(2)写出直线AB的解析式,并解释点C的实际意义;
(3)求a,b的值,并求出小明家所处的楼层.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察由棱长为 ![]() 的小立方体摆成的图形,寻找规律:如图 ① 中,共有
的小立方体摆成的图形,寻找规律:如图 ① 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ② 中,共有
个看不见;如图 ② 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ③ 中,共有
个看不见;如图 ③ 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;
个看不见; ![]() ,则第 ⑥个图中,看得见的小立方体有________________个.
,则第 ⑥个图中,看得见的小立方体有________________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北方某水果商店从南方购进一种水果,其进货成本是每吨0.4万元,根据市场调查这种水果在北方市场上的销售量y(吨)与每吨的销售价x(万元)之间的函数关系如下图所示:
(1)求出销售量y与每吨销售价x之间的函数关系式;
(2)如果销售利润为w(万元),请写出w与x之间的函数关系式;
(3)当每吨销售价为多少万元时,销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某保温杯专卖店通过市场调研,准备销售![]() 、
、![]() 两种型号的保温杯,其中每件
两种型号的保温杯,其中每件![]() 种保温杯的进价比
种保温杯的进价比![]() 种保温杯的进价高20元,已知专卖店用3200元购进
种保温杯的进价高20元,已知专卖店用3200元购进![]() 种保温杯的数量与用2560元购进
种保温杯的数量与用2560元购进![]() 种保温杯的数量相同.
种保温杯的数量相同.
(1)求两种保温杯的进价;
(2)若![]() 种保温杯的售价为250元,
种保温杯的售价为250元,![]() 种保温杯的售价为180元,专卖店共进两种保温杯200个,设
种保温杯的售价为180元,专卖店共进两种保温杯200个,设![]() 种保温杯进货
种保温杯进货![]() 个,求该专卖店获得的总利润
个,求该专卖店获得的总利润![]() (元)与
(元)与![]() 种保温杯进货数
种保温杯进货数![]() (个)之间的函数关系式,并写出自变量的取值范围.
(个)之间的函数关系式,并写出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax+![]() 与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点.
与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点.

(1)如图1,求抛物线的顶点坐标;
(2)如图2,点P为抛物线对称轴右侧上的一动点,过点P作PQ⊥AC于点Q,设点P的横坐标为t,点Q的横坐标为m,求m与t的函数关系式;
(3)在(2)的条件下,如图3,连接AP,过点C作CE⊥AP于点E,连接BE、CE分别交PQ于F、G两点,当点F是PG中点时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com