Question

6．△ABC中，AB=7，AC=5，则中线AD之长的范围是（　　）

• A． 5＜AD＜7
• B． 1＜AD＜6
• C． 2＜AD＜12
• D． 2＜AD＜5

Answer 1

分析 先作辅助线，延长AD至点E，使DE=AD，连接EC，先证明△ABD≌△ECD，在△AEC中，由三角形的三边关系定理得出答案．

解答 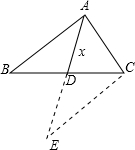解：延长AD至点E，使DE=AD，连接EC，
∵在△ABD和△ECD中
$\left\{\begin{array}{l}{BD=DC}\\{∠ADB=∠CDE}\\{AD=DE}\end{array}\right.$，
∴△ABD≌△ECD（SAS），
∴CE=AB，
∵AB=7，AC=5，CE=7，
设AD=x，则AE=2x，
∴2＜2x＜12，
∴1＜x＜6，
∴1＜AD＜6．
故选：B．

点评 本题考查了三角形的三边关系定理，难度一般，关键是掌握三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边．