
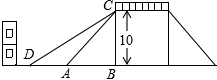
 如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 分析 需要拆除,理由为:根据题意得到三角形ABC为等腰直角三角形,求出AB的长,在直角三角形BCD中,根据新坡面的坡度求出∠BDC的度数为30,利用30度所对的直角边等于斜边的一半求出DC的长,再利用勾股定理求出DB的长,由DB-AB求出AD的长,由AD+3与10比较即可得到结果.
解答 解:需要拆除,理由为:
∵CB⊥AB,∠CAB=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=10米,
在Rt△BCD中,新坡面DC的坡度为i=$\sqrt{3}$:3,即∠CDB=30°,
∴DC=2BC=20米,BD=$\sqrt{C{D}^{2}-B{C}^{2}}$=10$\sqrt{3}$米,
∴AD=BD-AB=(10$\sqrt{3}$-10)米≈7.32米,
∵3+7.32=10.32>10,
∴需要拆除.
点评 此题考查了解直角三角形的应用-坡度坡角问题,涉及的知识有:勾股定理,等腰直角三角形的性质,含30度直角三角形的性质,坡角与坡度之间的关系,熟练掌握性质及定理是解本题的关键.


科目:初中数学 来源: 题型:解答题
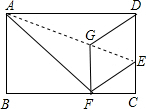 如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.
如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A 类 | 50 | 25 |
| B 类 | 200 | 20 |
| C 类 | 400 | 15 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
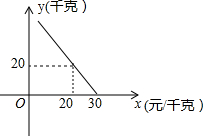 某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
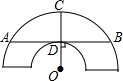 如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm.
如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,点A的坐标(-3,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD
如图,平面直角坐标系中,点A的坐标(-3,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com