
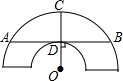
 如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm.
如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )| A. | 2 | B. | 2.8 | C. | 3 | D. | 3.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
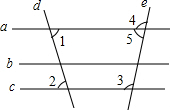 如图,下列说法错误的是( )
如图,下列说法错误的是( )| A. | 若a∥b,b∥c,则a∥c | B. | 若∠1=∠2,则a∥c | ||
| C. | 若∠3=∠2,则b∥c | D. | 若∠3+∠5=180°,则a∥c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
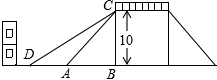 如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{-4}{-9}}$=$\frac{\sqrt{-4}}{\sqrt{-9}}$=$\frac{-2}{-3}$=$\frac{2}{3}$ | B. | $\sqrt{4\frac{2}{9}}$=$\sqrt{\frac{38}{9}}$=2$\frac{1}{3}$$\sqrt{2}$ | ||
| C. | $\sqrt{\frac{3}{7}}$÷$\sqrt{3\frac{1}{2}}$=$\frac{\sqrt{6}}{7}$ | D. | $\sqrt{\frac{8}{25}}$=5$\sqrt{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
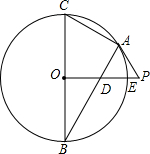 如图,已知PA与圆O相切于点A,直径BC⊥OP,线段OP与圆O交于点E,连接AB交PO于点D.
如图,已知PA与圆O相切于点A,直径BC⊥OP,线段OP与圆O交于点E,连接AB交PO于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
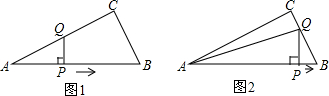
| A. | 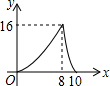 | B. | 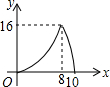 | C. | 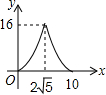 | D. | 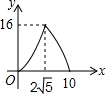 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com