
����Ŀ����֪��������x�ύ��A��6��0����B���� ![]() ��0�����㣬��y�ύ�ڵ�C�����������ϵ�M��1��3����MN��x���ڵ�N������OM��
��0�����㣬��y�ύ�ڵ�C�����������ϵ�M��1��3����MN��x���ڵ�N������OM�� 
��1����������ߵĽ���ʽ��
��2����ͼ1������OMN��x������ƽ��t����λ��0��t��5������O��M��N���λ�ã�MN�䡢M��O����ֱ��AC�ֱ��ڵ�E��F��
�ٵ���FΪM��O����е�ʱ����t��ֵ��
����ͼ2����ֱ��M��N�����������ཻ�ڵ�G������G��GH��M��O�佻AC�ڵ�H����ȷ���߶�EH�Ƿ�������ֵ�������ڣ�����������ֵ����ʱt��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�������߽���ʽΪy=a��x��6����x+ ![]() �����ѵ�M��1��3�������a=��
�����ѵ�M��1��3�������a=�� ![]() ��
��
�������߽���ʽΪy=�� ![]() ��x��6����x+
��x��6����x+ ![]() ����
����
��y=�� ![]() x2+
x2+ ![]() x+2��
x+2��
��2��
�⣺����ͼ1�У�AC��OM���ڵ�G������EO�䣮
��AO=6��OC=2��MN=3��ON=1��
�� ![]() =3��
=3��
�� ![]() ���ߡ�AOC=��MON=90�㣬
���ߡ�AOC=��MON=90�㣬
���AOC�ס�MNO��
���OAC=��NMO��
�ߡ�NMO+��MON=90�㣬
���MON+��OAC=90�㣬
���AGO=90�㣬
��OM��AC��
�ߡ�M��N��O�����ɡ�MNOƽ�����ã�
��O��M���OM��
��O��M���AC��
��M��F=FO�䣬
��EM��=EO�䣬
��EN���CO��
�� ![]() ��
��
�� ![]() ��
��
��EN��= ![]() ��5��t����
��5��t����
��RT��EO��M������O��N��=1��EN��= ![]() ��5��t����EO��=EM��=
��5��t����EO��=EM��= ![]() +
+ ![]() t��
t��
�ࣨ ![]() +
+ ![]() t��2=1+��
t��2=1+�� ![]() ��
�� ![]() t��2��
t��2��
��t=1��
����ͼ2�У�

��GH��O��M�䣬O��M���AC��
��GH��AC��
���GHE=90�㣬
�ߡ�EGH+��HEG=90�㣬��AEN��+��OAC=90�㣬��HEG=��AEN�䣬
���OAC=��HGE���ߡ�GHE=��AOC=90�㣬
���GHE�ס�AOC��
�� ![]() =
= ![]() ��
��
��EG���ʱ��EH���
��EG=GN�䩁EN��=�� ![]() ��t+1��2+
��t+1��2+ ![]() ��t+1��+2��
��t+1��+2�� ![]() ��5��t��=��
��5��t��=�� ![]() t2+
t2+ ![]() t+
t+ ![]() =��
=�� ![]() ��t��2��2+
��t��2��2+ ![]() ��
��
��t=2ʱ��EG���ֵ= ![]() ��
��
��EH���ֵ= ![]() ��
��
��t=2ʱ��EH���ֵΪ ![]() ��
��
����������1���������߽���ʽΪy=a��x��6����x+ ![]() �����ѵ�M��1��3�����뼴�����a������������⣮
�����ѵ�M��1��3�����뼴�����a������������⣮
��2������ͼ1�У�AC��OM���ڵ�G������EO�䣬����֤����AOC�ס�MNO���Ƴ�OM��AC����RT��EO��M���У����ù��ɶ����г����̼��ɽ�����⣮ ���ɡ�GHE�ס�AOC�� ![]() =
= ![]() =
= ![]() ������EG���ʱ��EH��������κ������EG�����ֵ���ɽ�����⣮���⿼����κ����ۺ��⡢���������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ��Ƿ���OM��CA��ѧ������ת����˼�������⣬ѧ�ṹ�����κ��������ֵ���⣬�����п�ѹ���⣮
������EG���ʱ��EH��������κ������EG�����ֵ���ɽ�����⣮���⿼����κ����ۺ��⡢���������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ��Ƿ���OM��CA��ѧ������ת����˼�������⣬ѧ�ṹ�����κ��������ֵ���⣬�����п�ѹ���⣮
�����㾫����������Ŀ����֪������������������������Ľ�������֪ʶ���Եõ�����Ĵ𰸣���Ҫ����һԪ���η��̵Ľ������Ӧ�Ķ��κ�����ͼ����x��Ľ������꣮���һԪ���η����е�b2-4ac���ڶ��κ����б�ʾͼ����x���Ƿ��н��㣮��b2-4ac>0ʱ��ͼ����x�����������㣻��b2-4ac=0ʱ��ͼ����x����һ�����㣻��b2-4ac<0ʱ��ͼ����x��û�н��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�Ǵ��ԲO��ֱ����AO��С��ԲM��ֱ������P�Ǵ��ԲO��һ�㣬PA��С��ԲM���ڵ�C������C��CD��OP�ڵ�D�� 
��1����֤��CD��С��ԲM�����ߣ�
��2����AB=8����P�ڴ��ԲO���˶�����P����A��B�����غϣ�����PD=x��CD2=y�� ����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
�ڵ�y=3ʱ����P��M����֮��ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD��BC���ϵĸߣ�BEƽ�֡�ABC��AC����E�������ཻ��F�㣮
��1������BAC=60�㣬��C=70�㣬���AFB�Ĵ�С��
��2����D��BC���е㣬��ABE=30�㣬��֤����ABC�ǵȱ������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� AD Ϊ�� ABC �����ߣ� BE Ϊ�� ABD �����ߣ�

��1���� ABE=15�㣬�� BED=55�㣬��� BAD �Ķ�����
��2������ BED �ı� BD ���ϵĸߣ�
��3������ ABC �����Ϊ 20�� BD=2.5����� BDE �� BD ���ϵĸ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵�������������
A. ���������ȵ�Բһ��ȫ��
B. ȫ����������ָ��״����С����ͬ��������
C. б�������ߺ�һ��ֱ�DZ߶�Ӧ��ȵ���ֱ��������ȫ��
D. �ױ���ȵ���������������ȫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��5��a��0����x�ύ�ڵ�A����5��0���͵�B��3��0������y�ύ�ڵ�C��
��1����������ߵĽ���ʽ��
��2������EΪx���·��������ϵ�һ���㣬��S��ABE=S��ABCʱ�����E�����ꣻ
��3���ڣ�2���������£����������Ƿ���ڵ�P��ʹ��BAP=��CAE�������ڣ������P�ĺ����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��4��a��0����x�ύ��A��4��0����B����1��0�����㣬����A��ֱ��y=��x+4���������ڵ�C��
��1����������ߵĽ���ʽ��
��2����ֱ��AC����һ����E������E��ij��λ��ʱ��ʹ��BDE���ܳ���С�����ʱE�����ꣻ
��3��������E��ֱ��AC��������Χ�ɵķ����A��C��B��D��A���˶�ʱ���Ƿ����ʹ��BDEΪֱ�������ε�����������ڣ���ֱ��д������Ҫ���E������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ֱ��������ABCֽƬ��б��AB�ϵ�����CD�������õ���ACD���ٽ���ACD��DB����ƽ�Ƶ���A��C��D���λ�ã���ƽ�ƿ�ʼ���D��δ�����Bʱ��A��C�佻CD��E��D��C�佻CB�ڵ�F������EF�����ı���EDD��FΪ����ʱ����̽����A��DE����״�����жϡ�A��DE���EFC���Ƿ�ȫ�ȣ���˵�����ɣ�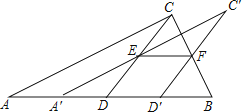
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ִ���С��A�ı�ƫ��60�㷽���С��80�����B����������������3Сʱ��С���ı�ƫ��45���C������ô���ʻ���ٶ�Ϊ����/Сʱ��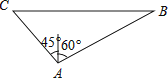
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com