
 如图,抛物线y=ax2+bx+c经过点A(-3,0)、B(1,0)、C(0,3).
如图,抛物线y=ax2+bx+c经过点A(-3,0)、B(1,0)、C(0,3).分析 (1)用待定系数法求出a,b,c,即可求解;
(2)用S=S△AOP+S△COP-S△AOC计算即可;
(3)设M(0,m)先判定△AOM≌△MFD,求出m即可.
解答 解:(1)∵抛物线y=ax2+bx+c经过点A(-3,0)、B(1,0)、C(0,3).
∴$\left\{\begin{array}{l}{9a-3b+c=0}\\{a+b+c=0}\\{c=}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
∴抛物线y=-x2-2x+3;
(2)如图所示,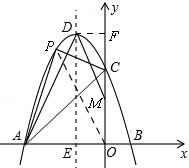
设P(x,-x2-2x+3),(-3<x<0),
∵OA=3,OC=3,
∴S=S△AOP+S△COP-S△AOC
=$\frac{1}{2}$OA×|yP|+$\frac{1}{2}$OA×|xP|-$\frac{1}{2}$OA×OC
=$\frac{1}{2}$×3×(-x2-2x+3)+$\frac{1}{2}$×3×(-x)-$\frac{1}{2}$×3×3
=-$\frac{3}{2}$x2-$\frac{9}{2}$x
=-$\frac{3}{2}$(x+$\frac{3}{2}$)2+$\frac{27}{8}$,
∴当x=-$\frac{3}{2}$时,S最大=$\frac{27}{8}$,
∴-(-$\frac{3}{2}$)2-2×(-$\frac{3}{2}$)+3=$\frac{15}{4}$,
∴点P的坐标为(-$\frac{3}{2}$,$\frac{15}{4}$),
(3)如图所示, 当△ADM是等腰直角三角形,只能∠AMD=90°,
当△ADM是等腰直角三角形,只能∠AMD=90°,
设M(0,m),过D作DF⊥x轴,
∴F(0,4),
∴OM=m,FM=4-m,DF=1,
∴△AOM≌△MFD,
∴OM=DF=1,FM=OA=3,
∴$\left\{\begin{array}{l}{m=1}\\{4-m=3}\end{array}\right.$,
∴m=1,
∴M(0,1)
点评 此题是二次函数综合题,主要考查了用待定系数法求函数解析式,三角形面积的计算方法,全等三角形的判定和性质,等腰直角三角形的性质,解本题的关键是熟记二次函数的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
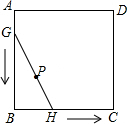 如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π.
如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
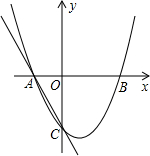 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的方程mx2-(3m-1)x+2m-2=0.
已知关于x的方程mx2-(3m-1)x+2m-2=0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
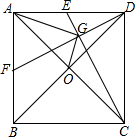 已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$.
已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.
如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com