
【题目】已知,如图,△ABC内接于⊙O,∠BAC=120°,AB=AC ,BD为⊙O的直径,AD=6 ,求BC的长

【答案】6.
【解析】
试题分析:首先过点O作OF⊥BC于F,由垂径定理可得BF=CF=![]() BC,然后由∠BAC=120°,AB=AC,利用等边对等角与三角形内角和定理,即可求得∠C与∠BAC的度数,由BD为⊙O的直径,即可求得∠BAD与∠D的度数,又由AD=6,即可求得BD的长,继而求得BC的长.
BC,然后由∠BAC=120°,AB=AC,利用等边对等角与三角形内角和定理,即可求得∠C与∠BAC的度数,由BD为⊙O的直径,即可求得∠BAD与∠D的度数,又由AD=6,即可求得BD的长,继而求得BC的长.
试题解析:过点O作OF⊥BC于F,

∴BF=CF=![]() BC,
BC,
∵AB=AC,∠BAC=120°,
∴∠C=∠ABC=![]() =30°,
=30°,
∵∠C与∠D是![]() 对的圆周角,
对的圆周角,
∴∠D=∠C=30°,
∵BD为⊙O的直径,
∴∠BAD=90°,
∴∠ABD=60°,
∴∠OBC=∠ABD-∠ABC=30°,
∵AD=6,
∴BD=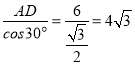 ,
,
∴OB=![]() BD=2
BD=2![]() ,
,
∴BF=OB×cos30°=2![]() ×
×![]() =3,
=3,
∴BC=6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图①,现有一张三角形ABC纸片,沿BC边上的高AE所在的直线翻折,使得点C与BC边上的点D重合.
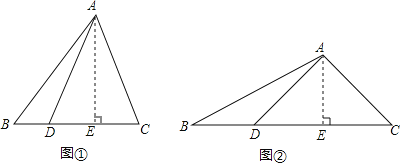
(1)填空:△ADC是 三角形;
(2)若AB=15,AC=13,BC=14,求BC边上的高AE的长;
(3)如图②,若∠DAC=90°,试猜想:BC、BD、AE之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】x表示一个两位数,y也表示一个两位数,君君想用x,y组成一个四位数,且把x放在y的右边,则这个四位数用代数式表示为( )
A. yx B. x+y C. 100x+y D. 100y+x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知样本数据x1 , x2 , x3 , …,xn的方差为4,则数据2x1+3,2x2+3,2x3+3,…,2xn+3的方差为( )
A.11
B.9
C.16
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某县七年级9800名学生的视力情况,从中抽查了100名学生的视力情况,就这个问题来说,下面说法正确的是( )
A. 9800名学生是总体 B. 每个学生是个体
C. 100名学生是所抽取的一个样本 D. 样本容量是100
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com