
 如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.
如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.分析 (1)由四边形ABCD是矩形,根据折叠的性质,易证得△EFG是等腰三角形,即可得GF=EC,又由GF∥EC,即可得四边形CEGF为平行四边形,根据邻边相等的平行四边形是菱形,即可得四边形BGEF为菱形;
(2)如图2,当G与A重合时,CE取最大值,由折叠的性质得CD=DG,∠CDE=∠GDE=45°,推出四边形CEGD是矩形,根据矩形的性质即可得到CE=CD=AB=3;如图1,当F与D重合时,CE取最小值,由折叠的性质得AE=CE,根据勾股定理即可得到结论.
解答 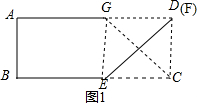 (1)证明:∵四边形ABCD是矩形,
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠GFE=∠FEC,
∵图形翻折后点G与点C重合,EF为折线,
∴∠GEF=∠FEC,
∴∠GFE=∠FEG,
∴GF=GE,
∵图形翻折后BC与GE完全重合,
∴BE=EC,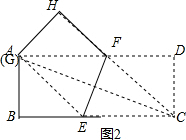
∴GF=EC,
∴四边形CEGF为平行四边形,
∴四边形CEGF为菱形;
(2)由(1)得四边形CEGF是菱形,
∴CE=CD=AB=3;
如图2,当G与A重合时,CE取最大值,
由折叠的性质得AE=CE,
∵∠B=90°,
∴AE2=AB2+BE2,即CE2=32+(9-CE)2,
∴CE=5,
∴线段CE的取值范围3≤CE≤5.
点评 本题考查了翻折变换-折叠问题,菱形的判定,线段的最值问题,矩形的性质,勾股定理,正确的作出图形是解题的关键.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
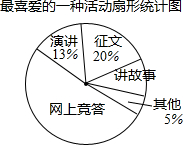 近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:| 活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
| 人数 | 60 | 30 | 39 | a | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com