
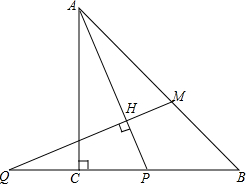
 在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.分析 (1)由等腰直角三角形的性质得出∠BAC=∠B=45°,∠PAB=45°-α,由直角三角形的性质即可得出结论;
(2)连接AQ,作ME⊥QB,由AAS证明△APC≌△QME,得出PC=ME,△MEB是等腰直角三角形,由等腰直角三角形的性质即可得出结论.
解答 解:(1)∠AMQ=45°+α;理由如下:
∵∠PAC=α,△ACB是等腰直角三角形,
∴∠BAC=∠B=45°,∠PAB=45°-α,
∵QH⊥AP,
∴∠AHM=90°,
∴∠AMQ=180°-∠AHM-∠PAB=45°+α;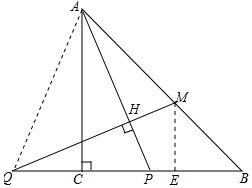
(2)PQ=$\sqrt{2}$MB;理由如下:
连接AQ,作ME⊥QB,如图所示:
∵AC⊥QP,CQ=CP,
∴∠QAC=∠PAC=α,
∴∠QAM=45°+α=∠AMQ,
∴AP=AQ=QM,
在△APC和△QME中,$\left\{\begin{array}{l}{∠MQE=∠PAC}&{\;}\\{∠ACP=∠QEM}&{\;}\\{AP=QM}&{\;}\end{array}\right.$,
∴△APC≌△QME(AAS),
∴PC=ME,
∴△MEB是等腰直角三角形,
∴$\frac{1}{2}$PQ=$\frac{\sqrt{2}}{2}$MB,
∴PQ=$\sqrt{2}$MB.
方法二:也可以延长AC到D,使得CD=CQ.
则易证△ADP≌△QBM.
∴BM=PD=$\sqrt{2}$CD=$\sqrt{2}$QC=$\frac{\sqrt{2}}{2}$PQ,
即PQ=$\sqrt{2}$MB.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理;熟练掌握等腰直角三角形的判定与性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
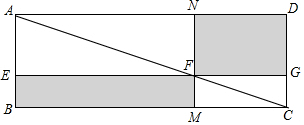 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com