
 如图,AB是⊙O的直径,弦CD⊥AB于点E,⊙O的半径为$\sqrt{3}$,弦CD的长为3cm,则图中阴影部分面积是π-$\frac{3\sqrt{3}}{4}$..
如图,AB是⊙O的直径,弦CD⊥AB于点E,⊙O的半径为$\sqrt{3}$,弦CD的长为3cm,则图中阴影部分面积是π-$\frac{3\sqrt{3}}{4}$.. 分析 根据垂径定理得到CE=$\frac{3}{2}$,根据勾股定理得到OE=$\frac{\sqrt{3}}{2}$,利用扇形和三角形的面积公式,求得阴影部分面积.
解答 解:∵弦CD⊥AB于点E,
∴CE=$\frac{3}{2}$,
∵OC=$\sqrt{3}$,
∴OE=$\frac{\sqrt{3}}{2}$,
∴∠OCE=30°,
∴∠COD=120°,
∴图中阴影部分面积=$\frac{120•π×(\sqrt{3})^{2}}{360}$-$\frac{1}{2}$×3×$\frac{\sqrt{3}}{2}$=π-$\frac{3\sqrt{3}}{4}$,
故答案为:π-$\frac{3\sqrt{3}}{4}$.
点评 本题主要考查了垂径定理,勾股定理,直角三角形的性质和扇形面积公式,数形结合是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
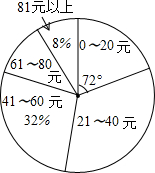 某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:| 捐款 | 人数 |
| 0~20元 | |
| 21~40元 | |
| 41~60元 | |
| 61~80元 | 6 |
| 81元以上 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 矩形的对角线相互垂直 | |
| B. | 顺次连结对角线相等的四边形各边中点所得到的四边形是矩形 | |
| C. | 等边三角形既是轴对称图形又是中心对称图形 | |
| D. | 对角线互相垂直平分的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 地铁站 | A | B | C | D | E |
| x(千米) | 8 | 9 | 10 | 11.5 | 13 |
| y1(分钟) | 18 | 20 | 22 | 25 | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (120-30$\sqrt{5}$)cm | B. | (160-60$\sqrt{5}$)cm | C. | (60$\sqrt{5}$-120)cm | D. | (60$\sqrt{5}$-6)cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 红红不是胜就是输,所以红红胜的概率为$\frac{1}{2}$ | |
| B. | 红红胜或娜娜胜的概率相等 | |
| C. | 两人出相同手势的概率为$\frac{1}{3}$ | |
| D. | 娜娜胜的概率和两人出相同手势的概率一样 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
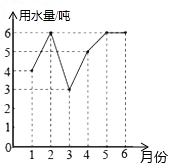 小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法中错误的( )
小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法中错误的( )| A. | 众数是6吨 | B. | 平均数是5吨 | C. | 中位数是5吨 | D. | 方差是$\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com