
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H. 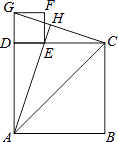
(1)求sin∠EAC的值.
(2)求线段AH的长.
【答案】
(1)解:作EM⊥AC于M.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC=3,∠DCA=45°,
∴在RT△ADE中,∵∠ADE=90°,AD=3,DE=1,
∴AE= ![]() ,
,
在RT△EMC中,∵∠EMC=90°,∠ECM=45°,EC=2,
∴EM=CM= ![]() ,
,
∴在RT△AEM中,sin∠EAM= ![]() =
= ![]() .
.

(2)在△GDC和△EDA中,
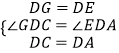 ,
,
∴△GDC≌△EDA,
∴∠GCD=∠EAD,GC=AE= ![]() ,
,
∵∠EHC=∠EDA=90°,
∴AH⊥GC,
∵S△AGC= ![]() AGDC=
AGDC= ![]() GCAH,
GCAH,
∴ ![]() ×4×3=
×4×3= ![]() ×
× ![]() ×AH,
×AH,
∴AH= ![]()
![]() .
.
【解析】(1)作EM⊥AC于M,根据sin∠EAM= ![]() 求出EM、AE即可解决问题.(2)先证明△GDC≌△EDA,得∠GCD=∠EAD,推出AH⊥GC,再根据S△AGC=
求出EM、AE即可解决问题.(2)先证明△GDC≌△EDA,得∠GCD=∠EAD,推出AH⊥GC,再根据S△AGC= ![]() AGDC=
AGDC= ![]() GCAH,即可解决问题.本题考查正方形的性质、全等三角形的判定和性质、勾股定理、三角形面积等知识,添加常用辅助线是解决问题的关键,学会用面积法求线段,属于中考常考题型.
GCAH,即可解决问题.本题考查正方形的性质、全等三角形的判定和性质、勾股定理、三角形面积等知识,添加常用辅助线是解决问题的关键,学会用面积法求线段,属于中考常考题型.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF. 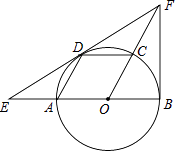
(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.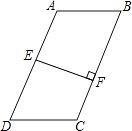
(1)若AB=DC,则四边形ABCD的面积S=;
(2)若AB>DC,则此时四边形ABCD的面积S′ S(用“>”或“=”或“<”填空).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①![]() BCD≌
BCD≌![]() CBE;②
CBE;②![]() BAD≌
BAD≌![]() BCD;③
BCD;③![]() BDA≌
BDA≌![]() CEA;④
CEA;④![]() BOE≌
BOE≌![]() COD;⑤
COD;⑤ ![]() ACE≌
ACE≌![]() BCE;上述结论一定正确的是
BCE;上述结论一定正确的是

A. ①②③ B. ②③④ C. ①③⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,利用尺规,根据下列要求作图(保留作图痕迹,不写作法),并根据要求填空:
(1)作∠ABC的平分线BD交AC于点D;
(2)作BD的垂直平分线交AB于E,交BC于F;
(3)在(1)、(2)条件下,连接DE,线段DE与线段BF的关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为![]() ,宽为
,宽为![]() (a>b>2)的长方形纸片上的四个角处各剪去一个边长为1的小正方形,然后做成一个无盖的长方体盒子.
(a>b>2)的长方形纸片上的四个角处各剪去一个边长为1的小正方形,然后做成一个无盖的长方体盒子.
(1)做成的长方体盒子的体积为 (用含![]() 的代数式表示);
的代数式表示);
(2)若长方形纸片的周长为30,面积为100,求做成的长方体盒子的体积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com