
如图,已知抛物线 图象经
图象经 过A(-1,0),B(4,0)两点.
过A(-1,0),B(4,0)两点.
(1)求抛物线的解析式;
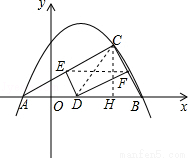
(2)若C(m,m-1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.

(1) ;(2)①证明见解析;②2.
;(2)①证明见解析;②2.
【解析】
试题分析:(1)根据待定系数法即可求得;
(2)把C(m,m-1)代入 求得点C的坐标,从而求得AH=4,CH=2,BH=1,AB=5,然后根据
求得点C的坐标,从而求得AH=4,CH=2,BH=1,AB=5,然后根据 ,∠AHC=∠BHC=90°得出△AHC∽△CHB,根据相似三角形的对应角相等求得∠ACH=∠CBH,因为∠CBH+∠BCH=90°所以∠ACH+∠BCH=90°从而求得∠ACB=90°,先根据有两组对边平行的四边形是平行四边形求得四边形DECF是平行四边形,进而求得
,∠AHC=∠BHC=90°得出△AHC∽△CHB,根据相似三角形的对应角相等求得∠ACH=∠CBH,因为∠CBH+∠BCH=90°所以∠ACH+∠BCH=90°从而求得∠ACB=90°,先根据有两组对边平行的四边形是平行四边形求得四边形DECF是平行四边形,进而求得 DECF是矩形;
DECF是矩形;
(3)根据矩形的对角线相等,求得EF=CD,因为当CD⊥AB时,CD的值最小,此时CD的值为2,所以EF的最小值是2;
试题解析:(1)∵抛物线 图象经过A(-1,0),B(4,0)两点,
图象经过A(-1,0),B(4,0)两点,
∴根据题意,得 ,解得
,解得 ,
,
所以抛物线的解析式为: ;
;
(2)①证明:∵把C(m,m-1)代入 得
得
∴ ,
,
解得:m=3或m=-2,
∵C(m,m-1)位于第一象限,
∴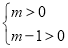 ,
,
∴m>1,
∴m=-2舍去,
∴m=3,
∴点C坐标为(3,2),
由A(-1,0)、B(3,0)、C(3,2)得 AH=4,CH=2,BH=1,AB=5
过C点作CH⊥AB,垂足为H,则∠AHC=∠BHC=90°,
∵ ,∠AHC=∠BHC=90°
,∠AHC=∠BHC=90°
∴△AHC∽△CHB,
∴∠ACH=∠CBH,
∵∠CBH+∠BCH=90°
∴∠ACH+∠BCH=90°
∴∠ACB=90°,
∵DE∥BC,DF∥AC,
∴四边形DECF是平行四边形,
∴ DECF是矩形;
DECF是矩形;
②存在;
连接CD
∵四边形DECF是矩形,
∴EF=CD,
当CD⊥AB时,CD的值最小,
∵C(3,2),
∴DC的最小值是2,
∴EF的最小值是2;
考点:二次函数综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.
(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:选择题
某商场对上月笔袋销售的情况进行统计如下表所示:
颜色 | 白色 | 黄色 | 蓝色 | 紫色 | 红色 |
数量(个) | 56 | 128 | 520 | 210 | 160 |
经理决定本月进笔袋时多进一些蓝色的,经理的这一决定应用了哪个统计知识( )
A.平均数 B.方差 C.中位数 D.众数
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建三明卷)数学(解析版) 题型:解答题
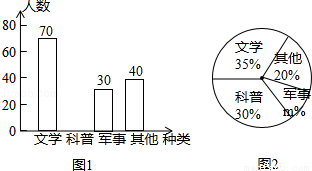
某学校在开展“书香校园”活动期间,对学生课外阅读的喜好进行抽样调查(每人只选一种书籍),将调查结果绘制成如图所示的两幅不完整的统计图,根据图中的信息,解答下列问题:
(1)这次调查的学生人数为 人,扇形统计图中m的值为 ;
(2)补全条形统计图;
(3)如果这所学校要添置学生课外阅读的书籍1500册,请你估计“科普”类书籍应添置多少册比较合适?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃天水卷)数学(解析版) 题型:选择题
点A、B、C是平面内不在同一条直线上的三点,点D是平面内任意一点,若A、B、C、D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com