
如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.
(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.

(1)证明见解析;(2)28.
【解析】
试题分析:(1)根据旋转可得AE=CE,DE=EF,可判定四边形ADCF是平行四边形,然后证明DF⊥AC,根据对角线互相垂直的平行的判定得到四边形ADCF是菱形.
(2)利用勾股定理可得AB长,再根据中点定义可得AD=5,根据菱形的性质可得AF=FC=AD=5,进而可得答案.
试题解析:【解析】
(1)证明:∵将△ADE绕点E旋转180°得到△CFE,∴AE=CE,DE=EF.
∴四边形ADCF是平行四边形.
∵D、E分别为AB,AC边上的中点,
∴DE是△ABC的中位线.∴DE∥BC.
∵∠ACB=90°,∴∠AED=90°.∴DF⊥AC.
∴四边形ADCF是菱形.
(2)在Rt△ABC中,BC=8,AC=6,∴AB=10.
∵D是AB边上的中点,∴AD=5.
∵四边形ADCF是菱形,∴AF=FC=AD=5.
∴四边形ABCF的周长为8+10+5+5=28.
考点:1.面动旋转问题;2.菱形的判定和性质;3.旋转的性质;4.三角形中位线的判定和性质;4.平行的性质;5.勾股定理.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源:2014年初中毕业升学考试(贵州黔西卷)数学(解析版) 题型:选择题
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:解答题
如图,PA,PB分别与⊙O相切于点A,B,∠APB=60°,连接AO,BO.
(1) 所对的圆心角∠AOB= ;
所对的圆心角∠AOB= ;
(2)求证:PA=PB;
(3)若OA=3,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:填空题
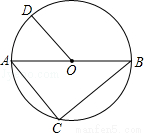
如图,AB是⊙O的直径,点D在⊙O上,∠BOD=130°,AC∥OD交⊙O于点C,连接BC,则∠B= 度.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:选择题
在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinA的值为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建南平卷)数学(解析版) 题型:解答题
如图,已知抛物线 图象经
图象经 过A(-1,0),B(4,0)两点.
过A(-1,0),B(4,0)两点.
(1)求抛物线的解析式;
(2)若C(m,m-1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com