Question

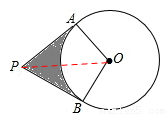
如图，PA，PB分别与⊙O相切于点A，B，∠APB=60°，连接AO，BO．

（1）所对的圆心角∠AOB= ；

（2）求证：PA=PB；

（3）若OA=3，求阴影部分的面积．

 

 

Answer 1

（1）120°；（2）证明见解析；（3）．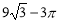

【解析】

试题分析：（1）根据切线的性质可以证得∠OAP=∠OBP=90°，根据四边形内角和定理求【解析】

∵PA，PB分别与⊙O相切于点A，B，∴∠OAP=∠OBP=90°．

∵∠APB=60°，∴∠AOB=180°﹣90°﹣90°﹣60°=120°．

（2）证明Rt△OAP≌Rt△OBP，根据全等三角形的对应边相等，即可证得．

（3）求得△OPA的面积和扇形OAB的面积，根据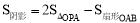求解．

试题解析：【解析】
（1）120°．

（2）证明：如答图，连接OP．

在Rt△OAP和Rt△OBP中，∵OA=OB，OP=OP，

∴Rt△OAP≌Rt△OBP（HL）．∴PA=PB；

（3）∵Rt△OAP≌Rt△OBP，

∴∠OPA=OPB=∠APB=30°，

在Rt△OAP中，OA=3，∴AP=．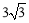

∴，．∴．

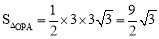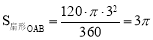考点：1．切线的性质；2．四边形内角和定理；3．全等三角形的判定和性质；4．三角形和扇形面积的计算；5．转换思想的应用．