
如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.

(1)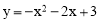 ,(﹣1,4);(2)
,(﹣1,4);(2)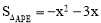 (﹣3<x<﹣1),
(﹣3<x<﹣1), ;(3)(
;(3)( ,
, ),点P′不在该抛物线上.
),点P′不在该抛物线上.
【解析】
试题分析:(1)由抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)两点,可设交点式,将点C的坐标代入求得a,b,c,进而得解析式,化为项点式可求顶点D.
(2)由P在AD上,则可求AD解析式表示P点.由 ,所以S可表示,进而由函数最值性质易得S最值.
,所以S可表示,进而由函数最值性质易得S最值.
(3)由最值时,P(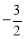 ,3),则E与C重合.画示意图,P'过作P'M⊥y轴,设边长通过解直角三角形可求各边长度,进而得P'坐标.判断P′是否在该抛物线上,将xP'坐标代入解析式,判断是否为yP'即可.
,3),则E与C重合.画示意图,P'过作P'M⊥y轴,设边长通过解直角三角形可求各边长度,进而得P'坐标.判断P′是否在该抛物线上,将xP'坐标代入解析式,判断是否为yP'即可.
试题解析:【解析】
(1)∵抛物线y=ax2+bx+c经过点A(﹣3,0)、B(1,0)两点,
∴可设抛物线解析式为 .
.
∵点C(0,3)在抛物线,∴ ,解得
,解得 .
.
∴抛物线的函数解析式为: ,即
,即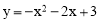 .
.
∵
∴抛物线顶点坐标D为(﹣1,4).
(2)设直线AD为解析式为 ,
,
∵A(﹣3,0),D(﹣1,4),
∴ ,解得
,解得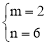 .
.
∴直线AD解析式:y=2x+6.
∵P在AD上,∴P(x,2x+6),
∴ (﹣3<x<﹣1).
(﹣3<x<﹣1).
∵ ,
,
当 时,S取最大值
时,S取最大值 .
.
(3)如图,设P′F与y轴交于点N,过P′作P′M⊥y轴于点M,
∵△PEF沿EF翻折得△P′EF,且P(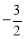 ,3),
,3),
∴∠PFE=∠P′FE,PF=P′F=3,PE=P′E= .
.
∵PF∥y轴,∴∠PFE=∠FEN.
∵∠PFE=∠P′FE,∴∠FEN=∠P′FE.
∴EN=FN.
设EN=m,则FN=m,P′N=3﹣m.
在Rt△P′EN中,∵ ,∴m=
,∴m= .
.
∵ ,
,
∴ ,解得
,解得 .
.
在Rt△EMP′中,∵ ,∴OM=EO﹣EM=
,∴OM=EO﹣EM= .
.
∴P′( ,
, ).
).
∵当x=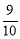 时,
时, ,
,
∴点P′不在该抛物线上.

考点:1.二次函数综合题;2.折叠问题;3.待定系数法的应用;3.曲线上点的坐标与方程的关系;4.二次函数的性质;5.由实际问题列函数关系式;6.折叠对称的性质;7.勾股定理.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源:2014年初中毕业升学考试(重庆A卷)数学(解析版) 题型:解答题
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(辽宁阜新卷)数学(解析版) 题型:选择题
在某校开展的“厉行节约,你我有责”活动中,七年级某班对学生7天内收集饮料瓶的情况统计如下(单位:个):76,90,64,100,84,64,73.则这组数据的众数和中位数分别是( )
A.64,100 B.64,76 C.76,64 D.64,84
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(辽宁抚顺卷)数学(解析版) 题型:选择题
下列事件是必然事件的是( )
A.如果|a|=|b|,那么a=b
B.平分弦的直径垂直于弦,并且平分弦所对的两条弧
C.半径分别为3和5的两圆相外切,则两圆的圆心距为8
D.三角形的内角和是360°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:解答题
如图,PA,PB分别与⊙O相切于点A,B,∠APB=60°,连接AO,BO.
(1) 所对的圆心角∠AOB= ;
所对的圆心角∠AOB= ;
(2)求证:PA=PB;
(3)若OA=3,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:选择题
六盘水市“琼都大剧院”即将完工,现需选用同一批地砖进行装修,以下不能镶嵌的地板是( )
A.正五边形地砖 B.正三角形地砖 C.正六边形地砖 D.正四边形地砖
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com