Question

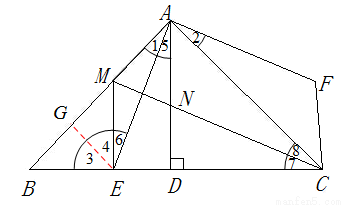
如图，△ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足是D，AE平分∠BAD，交BC于点E.在△ABC外有一点F，使FA⊥AE，FC⊥BC.

（1）求证：BE=CF；

（2）在AB上取一点M，使BM=2DE，连接MC，交AD于点N，连接ME.求证：①ME⊥BC；②DE=DN.

 

 

Answer 1

（1）证明见解析；（2）①证明见解析；②证明见解析.

【解析】

试题分析：（1）通过角的转换和等腰直角三角形的性质，得到∠BAE=∠CAF和∠B=∠FCA，从而ASA证明△ABF≌△ACF，根据全等三角形对应边相等得到结论.

（2）①过E点作EG⊥AB于点G，通过证明EG是BM的垂直平分线就易得出结论.

②通过证明Rt△AMC≌Rt△EMC和△ADE≌△CDN来证明结论.

试题解析：（1）如图，∵∠BAC=90°，FA⊥AE，∴∠1+∠EAC=90°，∠2+∠EAC=90°.

∴∠1=∠2.

又∵AB=AC，∴∠B=∠ACB=45°.

∵FC⊥BC，∴∠FCA=90°-∠ACB=45°.∴∠B=∠FCA.

∴△ABF≌△ACF（ASA）.∴BE=CF.

（2）①如图，过E点作EG⊥AB于点G，

∵∠B=45°，∴△CBE是等腰直角三角形.∴BG=EG，∠3=45°.

∵BM=2DE，∴BM=2BG，即点G是BM的中点.∴EG是BM的垂直平分线.∴∠4=∠3=45°.

∴∠MEB=∠4+∠3=90°.∴ME⊥BC.

②∵AD⊥BC，∴ME∥AD.∴∠5=∠6.

∵∠1=∠5，∴∠1=∠6.∴AM=EM.

∵MC=MC，∴Rt△AMC≌Rt△EMC（HL）.∴∠7=∠8.

∵∠BAC=90°，，AB=AC，∴∠ACB=45°，∠BAD=∠CAD=45°.

∴∠5=∠7=22.5°，AD=CD.

∵∠ADE=∠CDN=90°，∴△ADE≌△CDN（ASA）.∴DE=DN.

考点：1.等腰直角三角形的判定和性质；2.全等三角形的判定和性质；3.线段垂直平分线的判定和性质.