
| A. | 20° | B. | 80° | C. | 20°或80° | D. | 不能确定 |
分析 根据80°的角是顶角还是底角不确定,故应分两种情况进行讨论:(1)当80°的角是顶角时;(2)当80°的角是底角时;然后根据等腰三角形的两个底角相等,以及三角形的内角和定理,求出等腰三角形的顶角是多少即可.
解答 解:(1)当80°的角是顶角时,顶角是80°;
(2)当80°的角是底角时,
顶角的度数是:
180°-80°-80°
=100°-80°
=20°
综上,可得等腰三角形的顶角是20°或80°.
故选:C.
点评 (1)此题主要考查了等腰三角形的性质和应用,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是要明确:①等腰三角形的两腰相等.②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
(2)此题还考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 3.2×108元 | B. | 0.32×1010元 | C. | 3.2×109元 | D. | 32×108元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,C,D分别是线段AB,AC的中点,分别以点C,D为圆心,BC长为半径画弧,两弧交于点M,测量∠AMB的度数,结果为( )
如图,C,D分别是线段AB,AC的中点,分别以点C,D为圆心,BC长为半径画弧,两弧交于点M,测量∠AMB的度数,结果为( )| A. | 80° | B. | 90° | C. | 100° | D. | 105° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
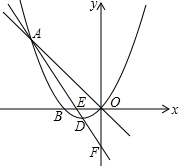 如图,已知二次函数y=ax2+bx+c(a≠0)的图象过原点O,与x轴相交于点B(-4,0),顶点为D,直线y=-x与二次函数的图象交于点A(m,8),直线AD交x轴于点E,交y轴于点F.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象过原点O,与x轴相交于点B(-4,0),顶点为D,直线y=-x与二次函数的图象交于点A(m,8),直线AD交x轴于点E,交y轴于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
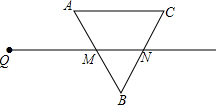 射线QN与边长为4的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,以点P为圆心,$\sqrt{3}$cm为半径的圆也随之移动.
射线QN与边长为4的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,以点P为圆心,$\sqrt{3}$cm为半径的圆也随之移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
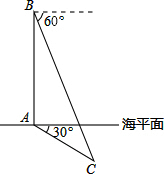 在一次军事演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方
在一次军事演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com