
分析 (1)令y=2x2+4x+5,则2x2+4x+5-y=0,然后根据△≥0,求出y的取值范围,即可求出二次三项式2x2+4x+5的最小值是多少.
(2)令m=-2x2+4x+3,则2x2-4x+m-3=0,然后根据△≥0,求出m的取值范围,即可求出y的取值范围.
解答 解:(1)令y=2x2+4x+5,
则2x2+4x+5-y=0,
∵2x2+4x+5-y=0有实数根,
∴△=42-4×2×(5-y)≥0,
∴y≥3,
∴二次三项式2x2+4x+5的最小值是3.
(2)令m=-2x2+4x+3,
则m≥0,
∴2x2-4x+m-3=0,
∵2x2-4x+m-3=0有实数根,
∴△=42-4×2×(m-3)≥0,
∴m≤5,
又∵m≥0,
∴0≤m≤5,
∴1≤$\sqrt{-2{x}^{2}+4x+3}$+1≤$\sqrt{5}$+1,
∴y的取值范围是:
1≤y≤$\sqrt{5}$+1.
点评 此题主要考查了二次函数的最值的求法,要熟练掌握,解答此题的关键是要明确:确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.


科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
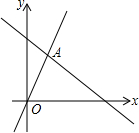 如图,函数y=kx和y=-$\frac{1}{2}$x+4的图象相交于点A(3,m)则不等式kx≥-$\frac{1}{2}$x+4的解集为( )
如图,函数y=kx和y=-$\frac{1}{2}$x+4的图象相交于点A(3,m)则不等式kx≥-$\frac{1}{2}$x+4的解集为( )| A. | x≥3 | B. | x≤3 | C. | x≤2 | D. | x≥2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )| A. | 3:2 | B. | 3:1 | C. | 1:1 | D. | 1:2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
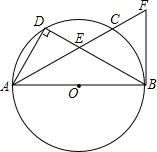 如图,AB是⊙O的直径,点C在⊙O上,点D是$\widehat{AC}$的中点,连接AD,BD.射线AC与BD相交于点E,与⊙O过点B的切线相交于点F,DE=4,BE=8.
如图,AB是⊙O的直径,点C在⊙O上,点D是$\widehat{AC}$的中点,连接AD,BD.射线AC与BD相交于点E,与⊙O过点B的切线相交于点F,DE=4,BE=8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com