
分析 根据一组对边平行且相等的四边形为平行四边形作图1;根据对角线互相平分的四边形为平行四边形作图2;根据两组对边分别相等的四边形为平行四边形作图3;根据两组对边分别平行的四边形为平行四边形作图4.
解答 解:如图1,作∠1=∠2,AD=BC,则四边形ABCD为平行四边形;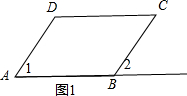
如图2,把线段AC和BD的中点重合,依次连结AB、BC、CD、DA,则四边形ABCD为平行四边形;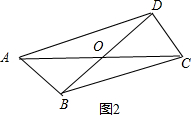
如图3,作∠BAD,使AB=a,AD=b,再分别以点D、B为圆心,以b和a为半径画弧,两弧相交于点C,则四边形ABCD为平行四边形;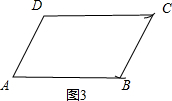 ;
;
如图4,作∠1=∠2,∠2=∠3,则四边形ABCD为平行四边形;,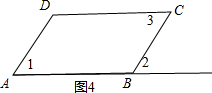 .
.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.充分利用平行四边形的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
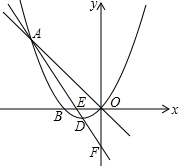 如图,已知二次函数y=ax2+bx+c(a≠0)的图象过原点O,与x轴相交于点B(-4,0),顶点为D,直线y=-x与二次函数的图象交于点A(m,8),直线AD交x轴于点E,交y轴于点F.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象过原点O,与x轴相交于点B(-4,0),顶点为D,直线y=-x与二次函数的图象交于点A(m,8),直线AD交x轴于点E,交y轴于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
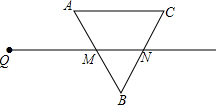 射线QN与边长为4的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,以点P为圆心,$\sqrt{3}$cm为半径的圆也随之移动.
射线QN与边长为4的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,以点P为圆心,$\sqrt{3}$cm为半径的圆也随之移动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (π-3.14)0是无理数 | B. | $\sqrt{(-5)^{2}}=-5$ | C. | (x2)2=x5 | D. | $(-\frac{1}{4})^{-2}=16$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com