
【题目】关于x的方程(k-1)x2+2kx+2=0
(1)求证:无论k为何值,方程总有实数根。
(2)设x1,x2是方程(k-1)x2+2kx+2=0的两个根,记S=![]() +
+![]() + x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。
+ x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。
【答案】(1)详见解析;(2)S的值能为2,此时k的值为2.
【解析】
试题分析:(1) 本题二次项系数为(k-1),可能为0,可能不为0,故要分情况讨论;要保证一元二次方程总有实数根,就必须使△>0恒成立;(2)欲求k的值,先把此代数式变形为两根之积或两根之和的形式,代入数值计算即可.
试题解析:⑴①当k-1=0即k=1时,方程为一元一次方程2x=1,
x=![]() 有一个解;
有一个解;
②当k-1≠0即k≠1时,方程为一元二次方程,
△=(2k)-4×2(k-1)=4k-8k+8=4(k-1) +4>0
方程有两不等根
综合①②得不论k为何值,方程总有实根
⑵∵x +x =![]() ,x x =
,x x =![]()
∴S=![]() +
+![]() + x1+x2
+ x1+x2
=![]()
=![]()
=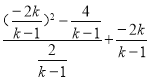
=![]()
=2k-2=2,
解得k=2,
∴当k=2时,S的值为2
∴S的值能为2,此时k的值为2.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知线段AB的两个端点分别是A(﹣4,﹣1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(﹣2,2),则点B′的坐标为( )
A.(4,3)
B.(3,4)
C.(﹣1,﹣2)
D.(﹣2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法).
(2)直接写出A′、B′、C′三点的坐标:
A′(); B′();
C′( ).
(3)求△ABC的面积 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在6×4的正方形网格中,点A、B、C、D、E、F都在格点上.连接点A、B得线段AB.
(1)连接C、D、E、F中的任意两点,共可得 条线段,在图中画出来;
(2)在(1)中所连得的线段中,与AB平行的线段是 ;
(3)用三角尺或量角器度量、检验,AB及(1)中所连得的线段中,互相垂直的线段有几对?(请用“⊥”表示出来) .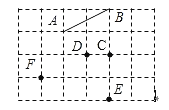
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1,x2,且满足![]() ,求实数p的值.
,求实数p的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com