
 如图,在?ABCD中,对角线BD、AC交于点O,∠ABD=2∠DBC,AE⊥BD于E.探究线段AB与OE的数量关系.
如图,在?ABCD中,对角线BD、AC交于点O,∠ABD=2∠DBC,AE⊥BD于E.探究线段AB与OE的数量关系. 分析 取AB的中点F,连接EF、OF,根据直角三角形斜边上的中线等于斜边的一半可得EF=BF=$\frac{1}{2}$AB,根据等边对等角可得∠ABD=∠BEF,根据三角形的中位线平行于第三边并且等于第三边的一半可得OF∥BC,根据两直线平行,内错角相等可得∠DBC=∠EOF,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠EFO=∠EOF,再根据等角对等边可得EF=OE,从而得证.
解答 解:AB=2OE,理由如下:
如图,取AB的中点F,连接EF、OF,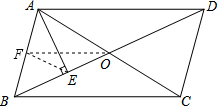 ∵AE⊥BD,
∵AE⊥BD,
∴EF=BF=$\frac{1}{2}$AB,
∴∠ABD=∠BEF,
∵AO=CO,
∴OF是△ABC的中位线,
∴OF∥BC,
∴∠DBC=∠EOF,
根据三角形的外角性质,∠BEF=∠EFO+∠EOF,
又∵∠ABD=2∠DBC,
∴∠EFO=∠EOF,
∴EF=OE,
∴OE=$\frac{1}{2}$AB,
∴AB=2OE.
点评 本题考查了平行四边形的对边平行,对角线互相平分的性质,直角三角形斜边上的中线等于斜边的一半,三角形的中位线平行于第三边并且等于第三边的一半,三角形的一个外角等于与它不相邻的两个内角的和的性质,作辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
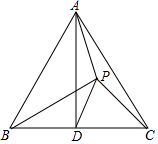 如图,△ABC是等边三角形,点D为BC的中点,点P在△ABC的内部,连接PA、PB、PC、PD,∠BPC=105°,PC=2,PB=2$\sqrt{2}$,则△APD的面积为$\frac{1}{2}\sqrt{3}$.
如图,△ABC是等边三角形,点D为BC的中点,点P在△ABC的内部,连接PA、PB、PC、PD,∠BPC=105°,PC=2,PB=2$\sqrt{2}$,则△APD的面积为$\frac{1}{2}\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,有一只蜗牛从直角坐标系的原点O向y轴正方向爬行,它前进1厘米后,右转90°,再前进1厘米后,左转90°,再前进1厘米后,右转90°,…当它走到点P(n,n)时,左边碰到障碍物,就直行1厘米,再右转90°,前进1厘米,再左转90°,前进1厘米,…最后回到x轴上,则蜗牛所走过的路程s为4n-1厘米.
如图所示,有一只蜗牛从直角坐标系的原点O向y轴正方向爬行,它前进1厘米后,右转90°,再前进1厘米后,左转90°,再前进1厘米后,右转90°,…当它走到点P(n,n)时,左边碰到障碍物,就直行1厘米,再右转90°,前进1厘米,再左转90°,前进1厘米,…最后回到x轴上,则蜗牛所走过的路程s为4n-1厘米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 解决问题:如图,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是10$\sqrt{2}$+8.
解决问题:如图,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是10$\sqrt{2}$+8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
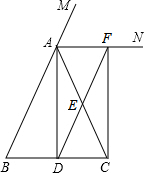 已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN是△ABC的外角∠CAM的平分线,E是AC的中点,连接DE并延长,交AN于F.
已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN是△ABC的外角∠CAM的平分线,E是AC的中点,连接DE并延长,交AN于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com