
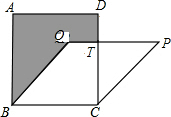
 如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )
如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )| A. | 23cm2 | B. | 33cm2 | C. | 43cm2 | D. | 53cm2 |
分析 先由正方形的面积求出边长,再由菱形的面积求出菱形的高,根据勾股定理求出PT和△CPT的面积,用整个图形的面积减去菱形的面积即为阴影部分的面积.
解答 解:∵正方形ABCD的面积为169cm2,
∴BC=$\sqrt{169}$=13,
又∵菱形BCPQ的面积为156cm2,
∴CT=$\frac{156}{13}$=12,CP=BC=13,
∴PT=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∴△CPT的面积=$\frac{1}{2}$×12×5=30,
∴阴影部分的面积=正方形ABCD的面积+△CPT的面积-菱形BCPQ=169+30-156=43(cm2),
故选:C.
点评 本题考查了菱形的性质、正方形的性质以及勾股定理的运用;熟练掌握面积的计算方法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
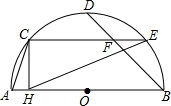 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、| A. | ①②③ | B. | 只有①② | C. | 只有①③ | D. | 只有③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
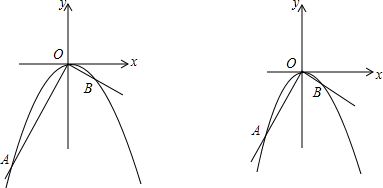
 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com