
如图,四边形ABCD是平行四边形,点A,B,C在⊙O上,AD与⊙O相切,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,且∠PCB=2∠BAF.

(1)求证:直线PC是⊙O的切线;
(2)若AB=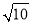 ,AD=2,求线段PC的长.
,AD=2,求线段PC的长.
(1)证明见试题解析;(2)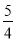 .
.
【解析】
试题分析:(1)连接OC,证明∠OCE+∠PCB=90°即可;
(2)由平行四边形的性质得到BC=2,根据垂径定理得到BE=1,再根据勾股定理得到AE=3,在Rt△OCE中,根据勾股定理得到半径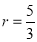 ,最后根据△OCE∽△CPE,得到PC的长.
,最后根据△OCE∽△CPE,得到PC的长.
试题解析:(1)连接OC.∵AD与⊙O相切于点A,∴FA⊥AD.∵四边形ABCD是平行四边形,∴AD∥BC,∴FA⊥BC,∵FA经过圆心O,∴F是 的中点,BE=CE,∠OEC=90°,∴∠COF=2∠BAF,∵∠PCB=2∠BAF,∴∠PCB=∠COF,∵∠OCE+∠COF=180°-∠OEC=90°,∴∠OCE+∠PCB=90°,∴OC⊥PC,∵点C在⊙O上,∴直线PC是⊙O的切线;
的中点,BE=CE,∠OEC=90°,∴∠COF=2∠BAF,∵∠PCB=2∠BAF,∴∠PCB=∠COF,∵∠OCE+∠COF=180°-∠OEC=90°,∴∠OCE+∠PCB=90°,∴OC⊥PC,∵点C在⊙O上,∴直线PC是⊙O的切线;

(2) ∵四边形ABCD是平行四边形,∴BC=AD=2,∴BE=CE=1,在Rt△ABE中,∠AEB=90°,
AB=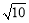 ,∴AE=
,∴AE= =3 ,设⊙O的半径为r,则OC=OA=r,OE=3-r, ,在Rt△OCE中,∠OEC=90°,∴
=3 ,设⊙O的半径为r,则OC=OA=r,OE=3-r, ,在Rt△OCE中,∠OEC=90°,∴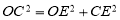 ,∴
,∴ 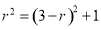 ,解得
,解得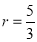 ,∵∠COE=∠PCE,∠OEC=∠CEP =90°,∴△OCE∽△CPE,∴
,∵∠COE=∠PCE,∠OEC=∠CEP =90°,∴△OCE∽△CPE,∴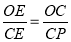 ,∴
,∴ ,∴
,∴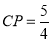 .
.
考点:1.切线的判定;2.相似三角形的判定与性质;3.垂径定理.


科目:初中数学 来源:2014-2015学年北京市通州区九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系中,A(-2,0),B(0,1),有一组抛物线 ,它们的顶点
,它们的顶点 在直线AB上,并且经过点
在直线AB上,并且经过点 ,当n = 1,2,3,4,5…时,
,当n = 1,2,3,4,5…时, ,3,5,8,13…,根据上述规律,写出抛物线
,3,5,8,13…,根据上述规律,写出抛物线 的表达式为___________,抛物线
的表达式为___________,抛物线 的顶点坐标为_________,抛物线
的顶点坐标为_________,抛物线 与
与 轴的交点坐标为__________________.
轴的交点坐标为__________________.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市石景山区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图1,平面直角坐标系 中,点
中,点 ,OC=8,若抛物线
,OC=8,若抛物线 平移后经过C,D两点,得到图1中的抛物线W.
平移后经过C,D两点,得到图1中的抛物线W.
(1)求抛物线W的表达式及抛物线W与 轴另一个交点
轴另一个交点 的坐标;
的坐标;
(2)如图2,以OA,OC为边作矩形OABC,连结OB,若矩形OABC从O点出发沿射线OB方向匀速运动,速度为每秒1个单位得到矩形 ,求当点
,求当点 落在抛物线W上时矩形的运动时间;
落在抛物线W上时矩形的运动时间;
(3)在(2)的条件下,如图3,矩形从O点出发的同时,点P从 出发沿矩形的边
出发沿矩形的边 以每秒
以每秒 个单位的速度匀速运动,当点P到达
个单位的速度匀速运动,当点P到达 时,矩形和点P同时停止运动,设运动时间为
时,矩形和点P同时停止运动,设运动时间为 秒.
秒.
①请用含 的代数式表示点P的坐标;
的代数式表示点P的坐标;
②已知:点P在边 上运动时所经过的路径是一条线段,求点P在边
上运动时所经过的路径是一条线段,求点P在边 上运动多少秒时,点D到CP的距离最大.
上运动多少秒时,点D到CP的距离最大.


查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市石景山区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,正方形ABCD的边长为a,动点P从点A出发,沿折线A→B→D→C→A的路径运动,回到点A时运动停止.设点P运动的路程长为x,AP长为y,则y关于x的函数图象大致是( )
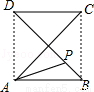
A.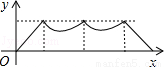
B.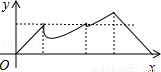
C.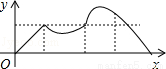
D.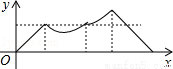
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市石景山区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinA的值是( )
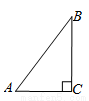
A. B.
B. C.
C.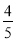 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:填空题
若扇形的半径为3cm,圆心角为120°,则这个扇形的面积为__________ cm2.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,矩形ABCD中,AP平分∠DAB,且AP⊥DP于点P,联结CP,如果AB﹦8,AD﹦4,求sin∠DCP的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com