
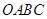 的直角顶点
的直角顶点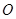 是坐标原点,边
是坐标原点,边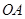 、
、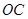 分别在
分别在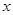 轴、
轴、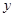 轴的正半轴上,
轴的正半轴上,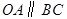 ,
,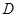 是
是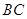 上一点,
上一点,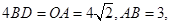
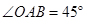 ,其中点
,其中点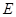 、
、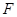 分别是线段
分别是线段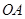 、
、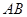 上的两个动点,且始终保持
上的两个动点,且始终保持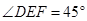 。
。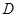 的坐标
的坐标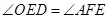 ;
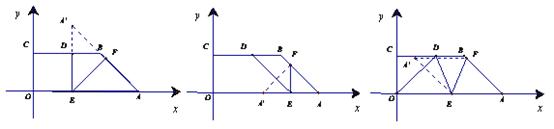
;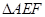 是等腰三角形时,△AEF关于直线EF的对称图形为
是等腰三角形时,△AEF关于直线EF的对称图形为 ,求
,求 与五边形OEFBC的重叠部分的面积.
与五边形OEFBC的重叠部分的面积.
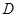
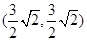 ..……..1分
..……..1分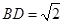 ,知
,知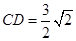 ,
,

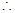
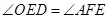
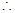
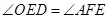 .……..3分
.……..3分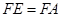 ,此时
,此时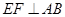 ,
,
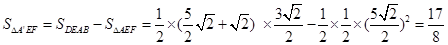 .……..4分
.……..4分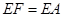 ,此时
,此时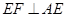 ,
, .……..5分
.……..5分 ,
,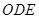 ,△
,△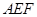 均为等腰三角形,
均为等腰三角形,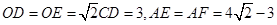
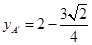 <
<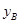 ,∴△
,∴△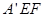 在五边形内部,
在五边形内部,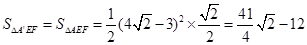 ..……..7分
..……..7分 =
=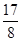 ,1,
,1,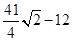 .
.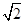 ,在Rt△ABM中,已知了∠OAB的度数及AB的长,即可求出AM、BM的长,进而可得到BC、CD的长,由此可求得D点的坐标;
,在Rt△ABM中,已知了∠OAB的度数及AB的长,即可求出AM、BM的长,进而可得到BC、CD的长,由此可求得D点的坐标;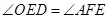 ;
;

 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
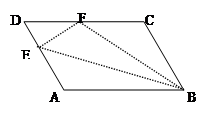
| A.5 | B.6 | C.7 | D.8 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
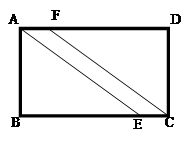
 以DE为折痕向右折叠,AE与BC交于点F,则
以DE为折痕向右折叠,AE与BC交于点F,则 的面积为( )
的面积为( )
| A.4 | B.6 | C.8 | D.10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com