
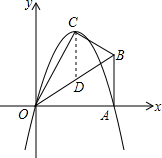
 如图,已知点A (2$\sqrt{3}$,0)、B(2$\sqrt{3}$,2).将△OAB沿OB折叠后,点A落在点c处,抛物线经过O、A、C三点,其对称轴与OB交于点D.
如图,已知点A (2$\sqrt{3}$,0)、B(2$\sqrt{3}$,2).将△OAB沿OB折叠后,点A落在点c处,抛物线经过O、A、C三点,其对称轴与OB交于点D.分析 (1)先在Rt△OAB中利用三角函数的定义求出∠AOB=30°,则利用折叠的性质得∠COB=∠AOB=30°,OC=OA=2$\sqrt{3}$,作CH⊥y轴于H,如图1,易∠COH=30°,根据含30度的直角三角形三边的关系得CH=$\frac{1}{2}$OC=$\sqrt{3}$,OH=$\sqrt{3}$CH=3,则C($\sqrt{3}$,3),然后设交点式y=ax(x-2$\sqrt{3}$),再把C点坐标代入求出a即可得到抛物线解析式为y=-x2+2$\sqrt{3}$x;
(2)如图1,先利用待定系数法求出直线OB的解析式为y=$\frac{\sqrt{3}}{3}$x,则可确定D($\sqrt{3}$,1),所以CD=2,利用二次函数图象上点的坐标特征、一次函数图象上点的坐标特征,设P(t,-t2+2$\sqrt{3}$t),则E(t,$\frac{\sqrt{3}}{3}$t),根据平行四边形的判定方法得PE=2,即|-t2+2$\sqrt{3}$t-$\frac{\sqrt{3}}{3}$t|=2,然后去绝对值解关于t的方程即可确定P点坐标;
(3)如图2,作FM⊥CD于M,QN⊥CD于N,利用二次函数图象上点的坐标特征、一次函数图象上点的坐标特征,设Q(x,$\frac{\sqrt{3}}{3}$x),则F(x,-x2+2$\sqrt{3}$x),根据等腰梯形的判定方法,当CM=ND时,四边形CDQF为等腰梯形,即3-(-x2+2$\sqrt{3}$x)=$\frac{\sqrt{3}}{3}$x-1,然后解此方程即可得到Q点坐标.
解答 解:(1)∵A (2$\sqrt{3}$,0)、B(2$\sqrt{3}$,2),
∴OA=2$\sqrt{3}$,AB=2,
∴tan∠AOB=$\frac{AB}{OA}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,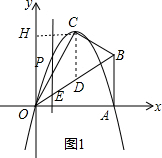
∴∠AOB=30°,
∵△OAB沿OB折叠后,点A落在点c处,
∴∠COB=∠AOB=30°,OC=OA=2$\sqrt{3}$,
作CH⊥y轴于H,如图1,∠COH=30°,
∴CH=$\frac{1}{2}$OC=$\sqrt{3}$,OH=$\sqrt{3}$CH=3,
∴C($\sqrt{3}$,3),
设抛物线解析式为y=ax(x-2$\sqrt{3}$),
把C($\sqrt{3}$,3)代入的a•$\sqrt{3}$(-$\sqrt{3}$)=3,解得a=-1,
∴抛物线解析式为y=-x(x-2$\sqrt{3}$),即y=-x2+2$\sqrt{3}$x;
(2)如图1,设直线OB的解析式为y=kx,
把B(2$\sqrt{3}$,2)代入得2$\sqrt{3}$k=2,解得k=$\frac{\sqrt{3}}{3}$,
∴直线OB的解析式为y=$\frac{\sqrt{3}}{3}$x,
当x=$\sqrt{3}$时,y=$\frac{\sqrt{3}}{3}$x=1,则D($\sqrt{3}$,1),
∴CD=2,
设P(t,-t2+2$\sqrt{3}$t),则E(t,$\frac{\sqrt{3}}{3}$t),
∴PE=|-t2+2$\sqrt{3}$t-$\frac{\sqrt{3}}{3}$t|=|t2-$\frac{5\sqrt{3}}{3}$t|,
∵点C、P、E、D为顶点的四边形为平行四边形,
而PE∥CD,
∴PE=2,即|t2-$\frac{5\sqrt{3}}{3}$t|=2,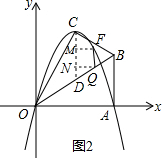
当t2-$\frac{5\sqrt{3}}{3}$t=2时,解得t1=$\frac{2\sqrt{3}}{3}$,t2=$\sqrt{3}$(舍去),此时P点坐标为($\frac{2\sqrt{3}}{3}$,$\frac{8}{3}$);
当t2-$\frac{5\sqrt{3}}{3}$t=-2时,解得t1=2$\sqrt{3}$,t2=-$\sqrt{3}$,此时P点坐标为(2$\sqrt{3}$,0)或(-$\sqrt{3}$,-3),
综上所述,以点C、P、E、D为顶点的四边形是平行四边形的点P有3个,它们是($\frac{2\sqrt{3}}{3}$,$\frac{8}{3}$),(2$\sqrt{3}$,0),(-$\sqrt{3}$,-3);
(3)存在.
如图2,作FM⊥CD于M,QN⊥CD于N,
设Q(x,$\frac{\sqrt{3}}{3}$x),则F(x,-x2+2$\sqrt{3}$x),
∵FQ∥CD,
∴当CM=ND时,四边形CDQF为等腰梯形,
即3-(-x2+2$\sqrt{3}$x)=$\frac{\sqrt{3}}{3}$x-1,
整理得x2-$\frac{7\sqrt{3}}{3}$x+4=0,解得x1=$\sqrt{3}$(舍去),x2=$\frac{4\sqrt{3}}{3}$,
此时Q点坐标为($\frac{4\sqrt{3}}{3}$,$\frac{4}{3}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、一次函数图象上点的坐标特征和折叠的性质;会利用待定系数法求函数的解析式;理解坐标与图形性质;熟悉平行四边形的性质和等腰梯形的判定方法;会解一元二次方程;学会运用分类讨论的思想解决数学问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 教练对明明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系满足y=a(x-4)2+h.
教练对明明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系满足y=a(x-4)2+h.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com