练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，△ABC中，∠C=70°，∠B=30°，将△ABC绕点A顺时针旋转后，得到△AB?C?，且C?在边BC上，则∠B?C?B的度数为（ ）

    A．30° B．40° C．50° D．60°

     

    B

    【解析】

    试题分析：根据旋转的性质可得：∠A C?B?=∠C=70°，A C= AC?，所以∠A C?C=∠C=70°,所以 ∠B?C?B=180°-70°-70°=40°.故选：B.

    考点：1. 旋转的性质；2.等腰三角形的性质；3.三角形的内角和.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014-2015学年北京市八年级上学期期中数学试卷（解析版） 题型：解答题

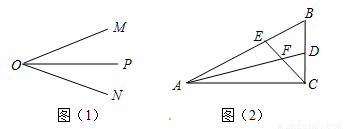
    （本题5分）（1）如图①，OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形。

    （2）请你参考这个作全等三角形的方法，解答下列问题：

    如图②，在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F。请你判断并写出FE与FD之间的数量关系并说明理由。

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年四川省仁寿县联谊学校七年级上学期期中考试数学试卷（解析版） 题型：计算题

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山西省九年级10月月考数学试卷（解析版） 题型：解答题

    如图，已知直线l的函数表达式为，且l与x轴、y轴分别交于A、B两点，动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动，同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动，设点Q、P移动时间为t秒。

    （1）求点A、B的坐标。

    （2）当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似？

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年天津市七年级上学期期中考试数学试卷（解析版） 题型：计算题

    －2 ＋（－2） －（－1）

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年天津市七年级上学期期中考试数学试卷（解析版） 题型：选择题

    3的相反数是（ ）

    A.-3 B.3 C. D.-

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年安徽省淮北市五校七年级上学期期中联考数学试卷（解析版） 题型：选择题

    下列为同类项的一组是（ ）

    A．与 B．与

    C．与 D．7与

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年安徽省淮北市五校联考八年级上学期期中考试数学试卷（解析版） 题型：解答题

    阅读理解题： 如图，在△ABC中，AD是BC边上的中线，且AD=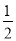BC．

    求证：∠BAC=90°．

    证明：∵AD=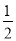BC，BD=CD=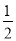BC，

    ∴AD=BD=DC，

    ∴ADB和 ADC都是等腰三角形

    ∴∠B=∠BAD，∠C=∠CAD，

    ∵∠B+∠BAD+∠CAD+∠C=180°，

    ∴∠BAD+∠CAD=90°，即∠BAC=90°．

    （1）此题实际上是直角三角形的另一个判定方法，请你用文字语言叙述出来．

    （2）直接运用这个结论解答题目：一个三角形一边长为2，这边上的中线长为1，另两边之和为1+，求这个三角形的面积．

    【知识储备：勾股定理：在直角三角形中。两直角边的平方和等于斜边的平方。】

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    下列条件中，能判定两个等腰三角形相似的是

    A．都含有一个30°的内角 B．都含有一个45°的内角 
    C．都含有一个60°的内角 D．都含有一个80°的内角 

    查看答案和解析>>

    同步练习册答案