
(本题5分)(1)如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形。
(2)请你参考这个作全等三角形的方法,解答下列问题:
如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F。请你判断并写出FE与FD之间的数量关系并说明理由。
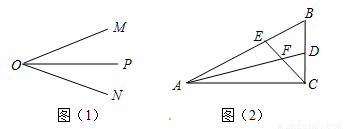
(1)见解析;(2)结论为EF=FD.
【解析】
试题分析:(1)由角平分线性质:角平分线上的点到两边的距离相等.得到一条边相等,由根据题目可知有一对角、公共角,所以在OP上任找一点E,过E分别做CE⊥OA于C,ED⊥OB于D,可得△OEC≌△OED.
(2)先证明△AEF≌△AGF(SAS).再证明∴△CFG≌△CFD(ASA).最后应用全等三角形的性质可得结论.
试题解析:(1)在OP上任找一点E,过E分别做CE⊥OA于C,ED⊥OB于D,可得△OEC≌△OED,如图①,

(2)结论为EF=FD.
如图②,在AC上截取AG=AE,连接FG.
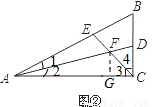
∵AD是∠BAC的平分线,
∴∠1=∠2,
在△AEF与△AGF中
AG=AE
∠1=∠2
AF=AF(公共边)
∴△AEF≌△AGF(SAS).
∴∠AFE=∠AFG,FE=FG.
由∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,
∵2∠2+2∠3+∠B=180°,
∴∠2+∠3=60°.
又∵∠AFE为△AFC的外角,
∴∠AFE=∠CFD=∠AFG=∠2+∠3=60°.
∴∠CFG=60°.
即∠GFC=∠DFC,
在△CFG与△CFD中
|
|
|
∴△CFG≌△CFD(ASA).
∴FG=FD.
∴FE=FD.
考点:角平分线的性质,全等三角形的判定、性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年云南省腾冲县九年级上学期五校联考摸底考试数学试卷(解析版) 题型:填空题
在Rt△ABC中,∠C=90°,sinB= ,则
,则 =________________;
=________________;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省仁寿县联谊学校七年级上学期期中考试数学试卷(解析版) 题型:选择题
在数轴上与点-2的距离为4的点所表示的数是( )
A、-6 B、2 C、±3 D、-6或2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省东莞市南开实验学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,△ABC中,∠C=70°,∠B=30°,将△ABC绕点A顺时针旋转后,得到△AB?C?,且C?在边BC上,则∠B?C?B的度数为( )

A.30° B.40° C.50° D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com