
【题目】如图1,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
(1)△BCE≌△CAD的依据是 (填字母);
(2)猜想:AD、DE、BE的数量关系为 (不需证明);
(3)当BE绕点B、AD绕点A旋转到图2位置时,线段AD、DE、BE之间又有怎样的数量关系,并证明你的结论.
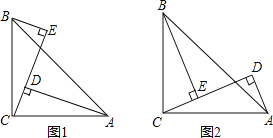
【答案】(1)AAS;(2)见解析;(3)DE=BE﹣AD.
【解析】
试题分析:(1)由题中条件求解△ACD≌△CBE,需要用到两个角和一个边;
(2)由题中条件求解△ACD≌△CBE,得出对应边相等,再利用线段之间的转化,进而可得出结论;
(3)中还是先求解△ACD≌△CBE,利用线段之间的转化得出结论.
(1)解:AAS.
(2)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥DE,
∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,又AC=BC,
∴△ACD≌△CBE(AAS),
∴AD=CE,BE=CD,
DE=CE﹣CD=AD﹣BE.
(3)解:DE=CD﹣CE=BE﹣AD.
证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥DE,
∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,又AC=BC,
∴△ACD≌△CBE(AAS),∴AD=CE,BE=CD,
DE=CD﹣CE=BE﹣AD.


科目:初中数学 来源: 题型:
【题目】数轴上一动点A向左移动3个单位长度到达点B,再向右移动4个单位长度到达点C,若点C表示的数为1,则点A表示的数为( )
A.7 B.1 C.0 D.﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级四个班级的学生义务为校植树.一班植树x棵,二班植树的棵树比一班的2倍少40棵,三班植树的棵数比二班的一半多30棵,四班植树的棵数比三班的一半多20棵.
(1)求四个班共植树多少棵?(用含x的式子表示)
(2)若三班和四班植树一样多,那么植树最多的班级比植树最少的班级多植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)求三辆车全部同向而行的概率;
(2)求至少有两辆车向左转的概率;
(3)由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为![]() ,向左转和直行的频率均为
,向左转和直行的频率均为![]() .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
.目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐标平面内下列各点中,在第三象限的点是( )
A. ( 1, 3 )
B. ( -3, 0 )
C. ( -1, 3 )
D. ( -1, -3 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
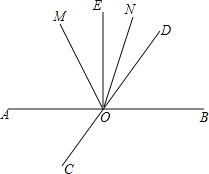
(1)若∠EON=18°,求∠AOC的度数.
(2)试判断∠MON与∠AOE的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com