
分析 (1)首先根据题意画出图形,根据平行四边形的性质证明∠2=∠3,∠6=∠4,再由条件BC=2AB,E为BC的中点证明∠1=∠2,∠5=∠6,再由平行四边形的性质可得∠2+∠6的度数,进而可得∠AED的度数;
(2)首先利用勾股定理计算出DE的长,然后再根据平行四边形ABCD的面积是△AED面积的2倍可得答案.
解答 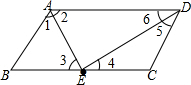 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠2=∠3,∠6=∠4,
∵BC=2AB,E为BC的中点,
∴AB=EB,EC=DC,
∴∠1=∠3,∠4=∠5,
∴∠1=∠2,∠5=∠6,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠1+∠2+∠6+∠5=180°,
∴∠2+∠6=90°,
∴∠AED=90°.
故答案为:90°;
(2)∵四边形ABCD是平行四边形,
∴AD=BC=4,
∵AE+AD=5,
∴AE=1,
∴ED=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{15}$,
∴S△AED=$\frac{1}{2}×$AE×ED=$\frac{\sqrt{15}}{2}$,
∴S?ABCD=$\sqrt{15}$.
故答案为:$\sqrt{15}$.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形对边平行,邻角互补.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,点P的坐标为(a,b),点P的“变换点”P′的坐标.定义如下:当a≥b时,P’点坐标为(b,-a);当a<b时,P′点坐标为(a,-b).
在平面直角坐标系xOy中,点P的坐标为(a,b),点P的“变换点”P′的坐标.定义如下:当a≥b时,P’点坐标为(b,-a);当a<b时,P′点坐标为(a,-b).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 分数段(分) | 15-19 | 20-24 | 25-29 | 30 |
| 人数 | 1 | 5 | 9 | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com