
分析 (1)可将该方程的已知根$\sqrt{5}$代入方程,求出m的值,即可求出方程的另一根,
(2)根据方程的两根恰为等腰三角形的两腰可得△=b2-4ac=0,列出式子,即可求实数m的值,再根据勾股定理可求底边的高,根据三角形面积公式计算即可求解.
解答 解:(1)∵x=$\sqrt{5}$是方程x2-4$\sqrt{5}$x+12+m=0的一个根
∴($\sqrt{5}$)2-4$\sqrt{5}$×$\sqrt{5}$+12+m=0
解得:m=3
则方程为:x2-4$\sqrt{5}$x+15=0
解得:x1=$\sqrt{5}$,x2=3$\sqrt{5}$.
∴方程的另一根为3$\sqrt{5}$.
(2)若方程的两根恰为等腰三角形的两腰,则△=b2-4ac=0,
所以△=(-4$\sqrt{5}$)2-4(12+m)=0,
解得m=8,
则方程为:x2-4$\sqrt{5}$x+20=0,
解得x=2$\sqrt{5}$,
底边的高为:$\sqrt{(3\sqrt{5})^{2}-(8÷2)^{2}}$=2,
故面积为8×2÷2=8.
点评 此题考查了一元二次方程的解和根的判别式,解决此类题目时要认真审题,根据根的判别式列出式子.


科目:初中数学 来源: 题型:填空题
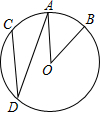 如图,点A,B,C,D分别在⊙O上,$\widehat{AB}$=$\widehat{AC}$,若∠AOB=40°,则∠ADC的大小是20度.
如图,点A,B,C,D分别在⊙O上,$\widehat{AB}$=$\widehat{AC}$,若∠AOB=40°,则∠ADC的大小是20度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某地进行城市规划,在一条新修 公路旁有一超市,现要建一个汽车站.为了超市距离车站最近,请你在公路上选一点来建汽车站,应建在( )
如图,某地进行城市规划,在一条新修 公路旁有一超市,现要建一个汽车站.为了超市距离车站最近,请你在公路上选一点来建汽车站,应建在( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE.若BD=3,CE=2,则△ABC的面积为( )
如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE.若BD=3,CE=2,则△ABC的面积为( )| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com