
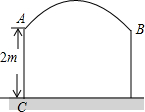
 某村想在村口建一个如图形状的牌门,已知弧$\widehat{AB}$是所在圆的三分之一圆,立柱AC高2m,若要使高3m,宽2m的集装箱货车能通过,问AB的半径应大于多少m?
某村想在村口建一个如图形状的牌门,已知弧$\widehat{AB}$是所在圆的三分之一圆,立柱AC高2m,若要使高3m,宽2m的集装箱货车能通过,问AB的半径应大于多少m? 分析 设货车顶部为MN,要使货车刚好能通过,则M、N在AB弧上,且MN∥AB,MN=2m,MN离地面高度为3m,设圆心为点O,圆的半径为x,连接OA、OM,作OF垂直AB,交圆于F,交AB于E,交MN于G,根据勾股定理得到OM2=OG2+MG2,即可求出AB的半径.
解答 解:设货车顶部为MN,要使货车刚好能通过,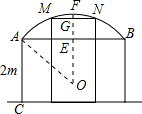
则M、N在AB弧上,且MN∥AB,MN=2m,MN离地面高度为3m,
设圆心为点O,圆的半径为x,连接OA、OM,作OF垂直AB,交圆于F,交AB于E,交MN于G,
则OF⊥MN,GE=3-2=1(m),
根据垂径定理知:MG=NG=1m,
$\widehat{AF}$=$\widehat{BF}$,
∵弧$\widehat{AB}$是所在圆的三分之一圆,
∴弧AF的度数=60°,
∴∠AOF=60°,∠OAE=30°,
∴OE=$\frac{OA}{2}$=$\frac{x}{2}$,
在直角三角形OMG中,根据勾股定理得:
OM2=OG2+MG2,
所以x2=1+($\frac{x}{2}$+1)2,
整理得:3x2-4x-8=0,
解得:x=$\frac{2±2\sqrt{7}}{3}$,
舍去负值得半径为$\frac{2+2\sqrt{7}}{3}$(m),
则弧AB的半径应大于$\frac{2+2\sqrt{7}}{3}$m
点评 本题考查了垂径定理的应用,与勾股定理相结合是解题的关键,要善于把实际问题与数学中的理论知识联系起来,能将生活中的问题抽象为数学问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com