
| A. | (-$\frac{7}{5}$,$\frac{4}{15}$) | B. | ($\frac{7}{5}$,-$\frac{4}{15}$) | C. | (-$\frac{7}{5}$,-$\frac{4}{15}$) | D. | ($\frac{7}{5}$,$\frac{4}{15}$) |
分析 如图,由图象可知,B、C、D共线,所以抛物线过A、B、D三点,设抛物线的解析式为y=ax2+bx+c,则有$\left\{\begin{array}{l}{c=3}\\{a+b+c=0}\\{9a+3b+c=4}\end{array}\right.$,求出抛物线的解析式,再求出顶点坐标即可.
解答 解:如图,由图象可知,B、C、D共线,
∴抛物线过A、B、D三点,
设抛物线的解析式为y=ax2+bx+c,则有$\left\{\begin{array}{l}{c=3}\\{a+b+c=0}\\{9a+3b+c=4}\end{array}\right.$,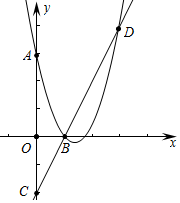
解得$\left\{\begin{array}{l}{a=\frac{5}{3}}\\{b=-\frac{8}{3}}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=$\frac{5}{3}$x2-$\frac{8}{3}$x+3=$\frac{5}{3}$(x-$\frac{7}{5}$)2-$\frac{4}{15}$,
∴顶点坐标为($\frac{7}{5}$,-$\frac{4}{15}$).
点评 本题考查二次函数的性质、待定系数法、配方法等知识,解题的关键是灵活运用所学知识解决问题,学会用配方法求顶点坐标,属于基础题.


科目:初中数学 来源: 题型:填空题
 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的距离分别为y甲(km)、y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图象如图所示,现有4种说法:①甲车的速度是80km/h;②乙车休息了1小时;③两车相距80km时,甲车行驶了3小时;④乙车两次行驶的速度相同.上述说法正确的有1个.
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的距离分别为y甲(km)、y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图象如图所示,现有4种说法:①甲车的速度是80km/h;②乙车休息了1小时;③两车相距80km时,甲车行驶了3小时;④乙车两次行驶的速度相同.上述说法正确的有1个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m(a+b)=ma+mb | B. | X2+2x+1=x(x+2)+1 | C. | (x+1)(x-1)=x2-1 | D. | x3-x=x(x+1)(x-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
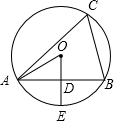 如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )
如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )| A. | AD=BD | B. | AE=BE | C. | AB=$\sqrt{3}$ | D. | OD=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边AC上一点O为圆心,OA为半径作圆,恰好经过边BC的中点D,并与边AC相交于另一点F.
如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边AC上一点O为圆心,OA为半径作圆,恰好经过边BC的中点D,并与边AC相交于另一点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com