
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]()
B.![]()
C.![]()
D.![]()
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:我们知道|x|= 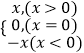 ,
,
所以当x>0时, ![]() =
= ![]() =1; 当x<0时,
=1; 当x<0时, ![]() =
= ![]() =﹣1.现在我们可以用这个结论来解决下面问题:
=﹣1.现在我们可以用这个结论来解决下面问题:
(1)已知a,b是有理数,当ab≠0时, ![]() +
+ ![]() =;
=;
(2)已知a,b是有理数,当abc≠0时, ![]() +
+ ![]() +
+ ![]() =;
=;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,则 ![]() +
+ ![]() +
+ ![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,
(1)若∠A=40°,∠B=60°,求∠DCE的度数.
(2)若∠A=m,∠B=n,求∠DCE.(用m、n表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点在格点上.

(1)画出△A1B1C1,使它与△ABC关于直线a对称;
(2)求出△A1B1C1的面积.
(3)在直线a上画出点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为确保信息安全,信息需加密传输,发送方由明文→密文(加密);接收方由密文→明文(解密).已知加密规则为:明文a,b,c,d对应的密文为a+b,b+c,c+d,d+2a.例如:明文1,2,3,4对应的密文为3,5,7,6.当接收方收到密文8,11,15,15时,则解密得到的明文应为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com