
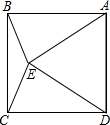
 如图,在正方形ABCD的内部作等边△ADE,连接BE、CE,求∠BEC的度数.
如图,在正方形ABCD的内部作等边△ADE,连接BE、CE,求∠BEC的度数.| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
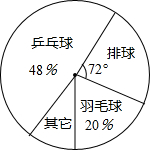 某班60名学生喜欢各类体育活动,他们最喜欢的一项体育活动情况见扇形统计图,现给出以下说法
某班60名学生喜欢各类体育活动,他们最喜欢的一项体育活动情况见扇形统计图,现给出以下说法| 1 |
| 5 |
| A、①②③ | B、①③④ |
| C、①②④ | D、①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、对角线相等,对边平行且相等 |
| B、一组对边平行,一组对角相等 |
| C、对角线互相平分且相等,对角线互相垂直 |
| D、一组邻边相等,对角线互相平分 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| x |
| 2 |
| x |
| A、x1=-1,x2=1 |
| B、x1=-1,x2=2 |
| C、x1=-2,x2=1 |
| D、x1=-1,x2=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
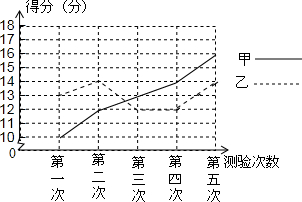 甲乙两人参加某体育项目训练,近期的五次测验得分情况(单位:分)如图所示
甲乙两人参加某体育项目训练,近期的五次测验得分情况(单位:分)如图所示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com