
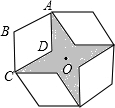
 如图是将菱形ABCD以点O为中心分别旋转90°,180°,270°后形成的图形,若∠BAD=60°,AB=2,则图中的阴影部分的面积为( )
如图是将菱形ABCD以点O为中心分别旋转90°,180°,270°后形成的图形,若∠BAD=60°,AB=2,则图中的阴影部分的面积为( )| A、8 | ||
B、12-4
| ||
C、1+
| ||
D、12-2
|
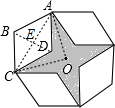 解:如图,连接AO、CO,连接AC和BD,交于点E
解:如图,连接AO、CO,连接AC和BD,交于点E| 3 |
| 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 6 |
| 1 |
| 4 |
| 3 |
| 3 |


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
| 1 | ||||
|
| 1 | ||||
|
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 5 |
| a2+b2+7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
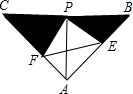 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③BE2+CF2=EF2,④S四边形AEPF=
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③BE2+CF2=EF2,④S四边形AEPF=| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
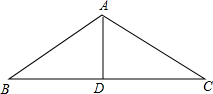 如图所示,在△ABC中,AB=AC,∠B=40°,若将△ABC沿∠BAC的角平分线剪开就成了两个小三角形,用这两个小三角形可以拼成多少种不同形状的四边形?画出示意图,并写出所拼成四边形的四个内角的度数.
如图所示,在△ABC中,AB=AC,∠B=40°,若将△ABC沿∠BAC的角平分线剪开就成了两个小三角形,用这两个小三角形可以拼成多少种不同形状的四边形?画出示意图,并写出所拼成四边形的四个内角的度数.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com