
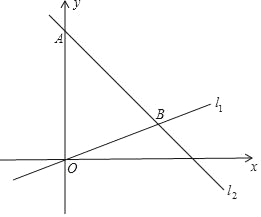
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�ڣ���A������Ϊ��0��8��������ԭ���ֱ��l1�뾭����A��ֱ��l2�ཻ�ڵ�B����B����Ϊ��6��2����
��1��ֱ��д��ֱ��l1�ı���ʽ�� ����l2�ı���ʽ�� ����
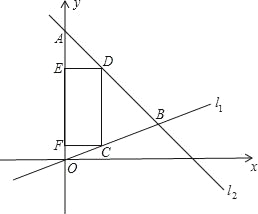
��2����CΪ�߶�0B��һ���㣨��C�����0��B�غϣ�����CD��y�ύֱ��l2�ڵ�D��
�����C�ĺ�����Ϊ3�����D������Ϊ�� ����
�����C�ĺ�����Ϊm�����D������Ϊ�� �������ú�m�Ĵ���ʽ��ʾ����
�������������£���CD=2����m��ֵΪ�� ����
���𰸡���1��y=![]() x��y=��x+8����2����D��3��5������D��m����m+8������
x��y=��x+8����2����D��3��5������D��m����m+8������![]() ��
��
��������
(1)����ֱ��l1�ı���ʽΪy=k1x����ֱ��l2�ı���ʽΪy=k2x+b����������뼴����������ʽ��
(2)�٢ڸ��ݵ�C��ֱ��l1�ϣ��ѵ�C�ĺ��������ֱ��l1�ı���ʽ���ɵó�C�����꣬����CD��y�ᣬ�ٸ��ݵ�D��ֱ��l2�ϼ��ɵó���D�ĺ����꣬�����ó����ۣ��۸���CD=2�з��̼��ɵõ����ۣ�
(1)��ֱ��l1�ı���ʽΪy=k1x��������6��2����6k1=2��k1=![]() ��
��
��y=![]() x��
x��
��ֱ��l2�ı���ʽΪy=k2x+b��������A��0��8����B��6��2����
��![]() ��
��
���![]() ��
��
��ֱ��l2�ı���ʽΪ��y=��x+8��
(2)��ͼ��
�١ߵ�C��ֱ��l1�ϣ��ҵ�C�ĺ�����Ϊ3��
��y=1��
���C��������3��1����
��CD��y�ᣬ
���D�ĺ�����Ϊ3��
�ߵ�D��ֱ��l2�ϣ�
��y=��3+8=5��
��D��3��5����
�ڡߵ�C��ֱ��l1�ϣ��ҵ�C�ĺ�����Ϊm��
��y=![]() m��
m��
���C��������m��![]() m����
m����
��CD��y�ᣬ
���D�ĺ�����Ϊm��
�ߵ�D��ֱ��l2�ϣ�
��y=��m+8��
��D��m����m+8����
�ۡ�CD=2��
����m+8��![]() m=2��
m=2��
��ã�m=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������г�Ϊ�˽���ֽγ��Ľ�������������г�ȥ��ɽ��Ķ��ֽγ���ȫ�����ݣ��Զ��ֽγ�����ǰ��ʹ��ʱ��Ϊ����ΪA��B��C��D��E���࣬��������Щ�����ɼף������˷ֱ���������������ͳ��ͼ��ͼ������������

�����������Ϣ������������⣺
��1�������������г�ȥ�깲�����ֽγ��� ������
��2�����������ͳ��ͼ��������������ͼ�����ע��Ӧ�����ݣ�
��3��������ͳ��ͼ�У�D����ֽγ�������������Ӧ���ε�Բ�Ľ�Ϊ�� ���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD�ı�AB��ADΪ�߷ֱ���������ȱ�������ABF��ADE������EB��FD������ΪG��
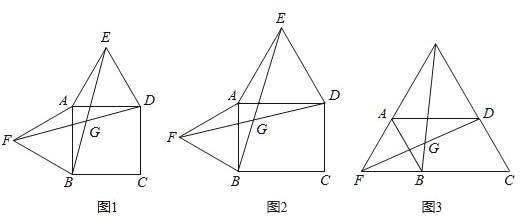
��1�����ı���ABCDΪ������ʱ����ͼ1����EB��FD��������ϵ���� ����
��2�����ı���ABCDΪ����ʱ����ͼ2����EB��FD����������������ϵ�������֤����
��3���ı���ABCD�������ε����ε�һ��ƽ���ı��εı仯�����У���EGD�Ƿ����仯������ı䣬��˵�����ɣ�������䣬����ͼ3�������EGD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ǹ���ij��2010����2014�깤ҵ������ֵ���Ƶ�����ͳ��ͼ���۲�ͳ��ͼ���������Ϣ��������Ϣ�жϴ�����ǣ� ��

A��2010����2014��乤ҵ������ֵ��������
B��2014��Ĺ�ҵ������ֵ��ǰһ��������40��Ԫ
C��2012����2013��ÿһ����ǰһ��ȣ�����������ͬ
D����2011����2014�꣬ÿһ����ǰһ��ȣ�2014������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�������η���ֽ�У�ÿ��С���ı��ζ�����ͬ�������Σ�A��B��C��D���ڸ�㴦��AB��CD�ཻ��O����tan��BOD��ֵ���� �� 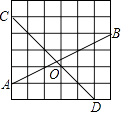
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪԭ�㣬ֱ��y=kx+b��x����A����3��0������y����B����������AOB�����Ϊ6����k=��������
A. ![]() B. ��
B. ��![]() C. ��4��4 D. ��
C. ��4��4 D. ��![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ȤС���ij�����꼶ѧ���г�ȡ2000�����������ʾ����飬�������������Ƴ���ͼ��ʾ������ͳ��ͼ��
�ʾ�
��ƽʱ��������(����)
A������ ������B����
��ѡ��Bѡ���ͬѧ�ش��������⣺
�������ٺ����ϵ�����������ʡ������Ǯ���ϣ�����̣���Ը��ƽ��ÿ���ٺ�(����)
A��0ƿ ������B��1ƿ
C��2ƿ ������D��2ƿ����

����������Ϣ������������⣺
(1)������ͼ��n��ֵ��
(2)���ÿƿ����ƽ��3ԪǮ�����ٺ�2ƿ���ϡ����ٺ�3ƿ���㣺
����2000��ѧ��һ�����ٺ������ܽ�ʡ����Ǯ���ϣ�����̣�
�ڰ�����ͳ�ƽ�����ƣ��������꼶6����ѧ��һ�����ٺ����ϴ�Լ�ܽ�ʡ����Ǯ���ϣ�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����������y=x��ͼ����һ�κ���y=kx��k��ͼ��Ľ�������ΪA��m��2����
��1����m��ֵ��һ�κ����Ľ���ʽ��
��2����һ�κ���y=kx��k��ͼ����y�ύ�ڵ�B�����AOB�������
��3��ֱ��д��ʹ����y=kx��k��ֵ���ں���y=x��ֵ���Ա���x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������εĶ��壬���Ƕ��壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı��Ρ���
��1����֪����ͼ1���ı���ABCD�ǡ��ȶԽ��ı��Ρ�����A�١�C����A=70�㣬��B=80�㣮���C����D�Ķ�����
��2����̽�����ȶԽ��ı��Ρ�����ʱ��
��С�컭��һ�����ȶԽ��ı��Ρ�ABCD����ͼ2�������С�ABC=��ADC��AB=AD����ʱ������CB=CD����������֤���˽��ۣ�
���ɴ�С����룺���������⡮�ȶԽ��ı��Ρ�����һ���ڱ����ʱ����һ���ڱ�Ҳ��ȡ�������Ϊ���IJ�����ȷ������ȷ����֤����������ȷ����ٳ�������
��3����֪���ڡ��ȶԽ��ı��Ρ�ABCD�У���DAB=60�㣬��ABC=90�㣬AB=5��AD=4����Խ���AC�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com