
ЁОЬтФПЁПЙХЯЃРАБЯДяИчРЫЙбЇХЩЕФЪ§бЇМвОГЃгУаЁЪЏзгАкГЩИїжжаЮзДРДбаОПЪ§бЇЮЪЬтЃЎ
ШчЭМ1ЃЌгЩгкетаЉШ§НЧаЮЪЧгЩ1ИіЃЌ3ИіЃЌ6ИіЃЌ10ИіЃЌЁ аЁЪЏзгАкГЩЕФЃЌЫљвдЫћУЧГЦ1ЃЌ3ЃЌ6ЃЌ10ЃЌЁЃЌетаЉЪ§ЮЊШ§БпаЮЪ§ЃЛРрЫЦЕФЃЌШчЭМ2ЃЌЫћУЧГЦ1ЃЌ4ЃЌ9ЃЌ16ЃЌЁЃЌетбљЕФЪ§ЮЊЫФБпаЮЪ§ЃЎ

ЃЈ1ЃЉМШЪЧШ§БпаЮЪ§ЃЌгжЪЧЫФБпаЮЪ§ЃЌЧвДѓгк1ЕФзюаЁе§ећЪ§ЪЧ ЃЛ
ЃЈ2ЃЉШчЙћМЧЕкnИіkБпаЮаЁЪЏзгЕФИіЪ§ЮЊ![]() ЃЈkЁн3ЃЉЃЌФЧУДвзЕУ
ЃЈkЁн3ЃЉЃЌФЧУДвзЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Ђй ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ
Ђк ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ
Ђл ШчЙћ![]() ЃЌФЧУД
ЃЌФЧУД![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЙћНјвЛВНбаОПЗЂЯж![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌФЧУД
ЃЌЁЃЌФЧУД![]() ЃЎ
ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ36ЃЛЃЈ2ЃЉЂй 6ЃЌ81ЃЛЂк![]() ЃЌ
ЃЌ![]() ЃЛЂл 10ЃЛЃЈ3ЃЉ1 000ЃЎ
ЃЛЂл 10ЃЛЃЈ3ЃЉ1 000ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЭМ1жа1ЁЂ3ЁЂ6ЁЂ10ЃЌЁЃЌЕкnИіЭМжаЕуЕФИіЪ§ЪЧ1+2+3+Ё+nЃЌМД![]() ЃЛЭМ2жа1ЁЂ4ЁЂ9ЁЂ16ЃЌЁЃЌЕкnИіЭМжаЕуЕФИіЪ§ЪЧn2ЃЌЧѓГіФмЭЌЪБТњзуСНИіЪНзгЕФЪ§ЃЌМДПЩЕУГіНсЙћЃЛ
ЃЛЭМ2жа1ЁЂ4ЁЂ9ЁЂ16ЃЌЁЃЌЕкnИіЭМжаЕуЕФИіЪ§ЪЧn2ЃЌЧѓГіФмЭЌЪБТњзуСНИіЪНзгЕФЪ§ЃЌМДПЩЕУГіНсЙћЃЛ
ЃЈ2ЃЉгЩЭМ1жа1ЁЂ3ЁЂ6ЁЂ10ЃЌЁЃЌЕкnИіЭМжаЕуЕФИіЪ§ЪЧ1+2+3+Ё+nЃЌМД![]() ЃЛЭМ2жа1ЁЂ4ЁЂ9ЁЂ16ЃЌЁЃЌЕкnИіЭМжаЕуЕФИіЪ§ЪЧn2ЃЌМДПЩЕУГіНсЙћЃЛ
ЃЛЭМ2жа1ЁЂ4ЁЂ9ЁЂ16ЃЌЁЃЌЕкnИіЭМжаЕуЕФИіЪ§ЪЧn2ЃЌМДПЩЕУГіНсЙћЃЛ
ЃЈ3ЃЉгЩMЃЈnЃЌ3ЃЉ![]() ЃЌMЃЈnЃЌ4ЃЉ
ЃЌMЃЈnЃЌ4ЃЉ![]() ЃЌMЃЈnЃЌ5ЃЉ
ЃЌMЃЈnЃЌ5ЃЉ![]() ЃЌMЃЈnЃЌ6ЃЉ
ЃЌMЃЈnЃЌ6ЃЉ![]() ЃЌПЩЭЦЖЯMЃЈnЃЌkЃЉ
ЃЌПЩЭЦЖЯMЃЈnЃЌkЃЉ![]() ЃЈkЁн3ЃЉЃЌНЋMЃЈ10ЃЌ24ЃЉДњШыМДПЩЕУГіНсЙћЃЎ
ЃЈkЁн3ЃЉЃЌНЋMЃЈ10ЃЌ24ЃЉДњШыМДПЩЕУГіНсЙћЃЎ
ЃЈ1ЃЉЁпЫФБпаЮЪ§ЕуЕФИіЪ§ЪЧЮЊn2ЃЌ
ЁрГ§1ЭтЃЌЗжБ№ЮЊ4ЃЌ9ЃЌ16ЃЌ25ЃЌ36ЃЌ49ЃЌ64ЃЌЁЃЎ
ЁпЭМ1жа1ЁЂ3ЁЂ6ЁЂ10ЃЌЁЃЌЕкnИіЭМжаЕуЕФИіЪ§ЪЧ1+2+3+Ё+nЃЌМДШ§БпаЮЪ§ЕуЕФИіЪ§ЪЧЮЊ![]() ЃЌ
ЃЌ
Ёп4![]() Юое§ећЪ§НтЃЌ
Юое§ећЪ§НтЃЌ
Ёр4ВЛЪЧШ§БпаЮЪ§ЃЎ
Ёп9![]() Юое§ећЪ§НтЃЌ
Юое§ећЪ§НтЃЌ
Ёр9ВЛЪЧШ§БпаЮЪ§ЃЎ
Ёп16![]() Юое§ећЪ§НтЃЌ
Юое§ећЪ§НтЃЌ
Ёр16ВЛЪЧШ§БпаЮЪ§ЃЎ
Ёп25![]() Юое§ећЪ§НтЃЌ
Юое§ећЪ§НтЃЌ
Ёр25ВЛЪЧШ§БпаЮЪ§ЃЎ
Ёп36![]() ЃЌНтЕУЃКn=8ЃЌЫљвд36ЪЧШ§БпаЮЪ§ЃЌ
ЃЌНтЕУЃКn=8ЃЌЫљвд36ЪЧШ§БпаЮЪ§ЃЌ
ЁрГ§1ЭтЃЌзюаЁЕФМШЪЧШ§БпаЮЪ§гжЪЧЫФБпаЮЪ§ЕФЪЧ36ЃЎ
ЙЪД№АИЮЊЃК36ЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊЃКMЃЈnЃЌ3ЃЉ![]() ЃЌMЃЈnЃЌ4ЃЉ=n2ЃЛ
ЃЌMЃЈnЃЌ4ЃЉ=n2ЃЛ
ЙЪЃКЂйMЃЈ3ЃЌ3ЃЉ=![]() =6ЃЌMЃЈ9ЃЌ4ЃЉ=92=81ЃЛ
=6ЃЌMЃЈ9ЃЌ4ЃЉ=92=81ЃЛ
ЂкMЃЈnЃЌ3ЃЉ![]() ЃЌMЃЈnЃЌ4ЃЉ=n2ЃЛ
ЃЌMЃЈnЃЌ4ЃЉ=n2ЃЛ
ЂлMЃЈnЃЌ3ЃЉ![]() =55ЃЌ
=55ЃЌ
Ёрn2+n-110=0ЃЌ
ЁрЃЈn-10ЃЉЃЈn+11ЃЉ=0ЃЌ
НтЕУЃКn=10Лђn=-11ЃЈЩсШЅЃЉЃЌ
Ёрn=10ЃЎ
ЃЈ3ЃЉЁпMЃЈnЃЌ3ЃЉ![]() ЃЌ
ЃЌ
MЃЈnЃЌ4ЃЉ=n2![]() ЃЌ
ЃЌ
MЃЈnЃЌ5ЃЉ![]() n2
n2![]() n
n![]() ЃЌ
ЃЌ
MЃЈnЃЌ6ЃЉ=2n2Љn![]() ЃЌ
ЃЌ
ЁргЩДЫБфЛЏЙцТЩПЩЭЦЖЯMЃЈnЃЌkЃЉ![]() ЃЈkЁн3ЃЉЃЌ
ЃЈkЁн3ЃЉЃЌ
ЁрMЃЈ10ЃЌ24ЃЉ![]() 1000ЃЎ
1000ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЪЧЪ§жсЩЯШ§ЕуЃЌЕу
ЪЧЪ§жсЩЯШ§ЕуЃЌЕу![]() ЮЊдЕуЃЌЕу
ЮЊдЕуЃЌЕу![]() БэЪОЕФЪ§ЮЊ6ЃЌ
БэЪОЕФЪ§ЮЊ6ЃЌ![]() ЃЌ
ЃЌ![]() .
.
![]()
ЃЈ1ЃЉаДГіЪ§жсЩЯЕу![]() ЁЂ
ЁЂ![]() БэЪОЕФЪ§ЃЛ
БэЪОЕФЪ§ЃЛ
ЃЈ2ЃЉЖЏЕу![]() ЁЂ
ЁЂ![]() ЗжБ№Дг
ЗжБ№Дг![]() ЁЂ
ЁЂ![]() ЭЌЪБГіЗЂЃЌбиЪ§жсЯђгвдШЫйдЫЖЏ.Еу
ЭЌЪБГіЗЂЃЌбиЪ§жсЯђгвдШЫйдЫЖЏ.Еу![]() ЕФЫйЖШЪЧУПУы6ИіЕЅЮЛГЄЖШЃЌЕу
ЕФЫйЖШЪЧУПУы6ИіЕЅЮЛГЄЖШЃЌЕу![]() ЕФЫйЖШЪЧУПУы3ИіЕЅЮЛГЄЖШЃЌЕу
ЕФЫйЖШЪЧУПУы3ИіЕЅЮЛГЄЖШЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌЩшдЫЖЏЪБМфЮЊ
ЃЌЩшдЫЖЏЪБМфЮЊ![]() Уы.
Уы.
ЂйЧѓЪ§жсЩЯЕу![]() ЁЂ
ЁЂ![]() БэЪОЕФЪ§ЃЈгУКЌ
БэЪОЕФЪ§ЃЈгУКЌ![]() ЕФЪНзгБэЪОЃЉЃЛ
ЕФЪНзгБэЪОЃЉЃЛ
ЂкЕБ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ИіЕужаЕФЦфжавЛИіЕуЪЧСэСНЕуЙЙГЩЕФЯпЖЮЕФжаЕуЕФЪБКђЃЌЧѓ
Ш§ИіЕужаЕФЦфжавЛИіЕуЪЧСэСНЕуЙЙГЩЕФЯпЖЮЕФжаЕуЕФЪБКђЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌБэжаИјГіЕФЪЧФГдТЕФдТРњЃЌШЮвтбЁШЁЁАUЁБаЭПђжаЕФ7ИіЪ§ЃЈШчвѕгАВПЗжЫљЪОЃЉЃЌЧыФудЫгУЫљбЇЕФЪ§бЇжЊЪЖРДбаОПЃЌЗЂЯжет7ИіЪ§ЕФКЭВЛПЩФмЕФЪЧ( )
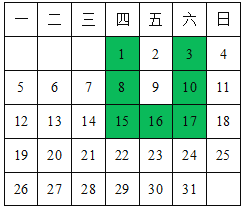
A.70B.78C.84D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊФГЯюЙЄГЬгЩМзввСНЖгКЯзї12ЬьПЩвдЭъГЩ,ЙЉашЙЄГЬЗбгУ13800дЊ,ввЖгЕЅЖРЭъГЩетЯюЙЄГЬЫљашЪБМфЪЧМзЖгЕЅЖРЭъГЩетЯюЙЄГЬЫљашЪБМфЕФ1.5БЖ,ЧвМзЖгУПЬьЕФЙЄГЬЗбгУБШввЖгЖр150дЊЁЃ
ЃЈ1ЃЉМзввСНЖгЕЅЖРЭъГЩетЯюЙЄГЬЗжБ№ашвЊЖрЩйЬь?
ЃЈ2ЃЉШєЙЄГЬЙмРэВПУХОіЖЈДгетСНИіЖгжабЁвЛИіЖгЕЅЖРЭъГЩетЯюЙЄГЬ,ДгНкдМзЪН№ЕФНЧЖШПМТЧ,гІИУбЁдёФФИіЙЄГЬЖг?ЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2019Фъ7дТ9ШеЃЌББОЉЪаЕЮЕЮПьГЕЕїећСЫМлИёЃЌЙцЖЈГЕЗбгЩЁАзмРяГЬЗб+змЪБГЄЗбЁБСНВПЗжЙЙГЩЃЌОпЬхЪеЗбБъзМШчЯТБэЃКЃЈзЂЃКШчЙћГЕЗбВЛзуЦ№ВНМлЃЌдђАДЦ№ВНМлЪеЗбЃЎЃЉ
ЪБМфЖЮ | РяГЬЗбЃЈдЊ/ЧЇУзЃЉ | ЪБГЄЗбЃЈдЊ/ЗжжгЃЉ | Ц№ВНМлЃЈдЊЃЉ |
06:00ЁЊ10:00 | 1.80 | 0.80 | 14.00 |
10:00ЁЊ17:00 | 1.45 | 0.40 | 13.00 |
17:00ЁЊ21:00 | 1.50 | 0.80 | 14.00 |
21:00ЁЊ06:00 | 2.15 | 0.80 | 14.00 |
ЃЈ1ЃЉаЁУї07:10ГЫПьГЕЩЯбЇЃЌааЪЛРяГЬ6ЧЇУзЃЌЪБГЄ10ЗжжгЃЌгІИЖГЕЗб дЊЃЛ
ЃЈ2ЃЉаЁЗМ17:20ГЫПьГЕЛиМвЃЌааЪЛРяГЬ1ЧЇУзЃЌЪБГЄ15ЗжжгЃЌгІИЖГЕЗб дЊЃЛ
ЃЈ3ЃЉаЁЛЊЭэздЯАКѓГЫПьГЕЛиМвЃЌ20:45дкбЇаЃЩЯГЕЃЎгЩгкЕРТЗЪЉЙЄЃЌГЕСОааЪЛЛКТ§ЃЌ15ЗжжгКѓбЁдёСэЭтЕРТЗЃЌИФЕРКѓЫйЖШЪЧИФЕРЧАЫйЖШЕФ3БЖЃЌ10ЗжжгКѓЕНМвЃЌЙВИЖСЫГЕЗб37.4дЊЃЌЮЪДгбЇаЃЕНаЁЛЊМвПьГЕааЪЛСЫЖрЩйЧЇУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЦпФъМЖПЊеЙеїЮФЛюЖЏЃЌеїЮФжїЬтжЛФмДгЁААЎЙњЁБЁАОДвЕЁБЁАГЯаХЁБЁАгбЩЦЁБЫФИіжїЬтбЁдёвЛИіЃЌЦпФъМЖУПУћбЇЩњАДвЊЧѓЖМЩЯНЛСЫвЛЗнеїЮФЃЌбЇаЃЮЊСЫНтбЁдёИїжжеїЮФжїЬтЕФбЇЩњШЫЪ§ЃЌЫцЛњГщШЁСЫВПЗжеїЮФНјааЕїВщЃЌИљОнЕїВщНсЙћЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМ.

ЃЈ1ЃЉЧѓЙВГщШЁСЫЖрЩйУћбЇЩњЕФеїЮФЃЛ
ЃЈ2ЃЉНЋЩЯУцЕФЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉдкЩШаЮЭГМЦЭМжаЃЌЁААЎЙњЁБжїЬтЫљЖдгІЕФдВаФНЧЪЧЖрЩйЃЛ
ЃЈ4ЃЉШчЙћИУаЃЦпФъМЖЙВга![]() УћбЇЩњЃЌЧыЙРМЦИУаЃбЁдёвдЁАгбЩЦЁБЮЊжїЬтЕФЦпФъМЖбЇЩњгаЖрЩйУћ.
УћбЇЩњЃЌЧыЙРМЦИУаЃбЁдёвдЁАгбЩЦЁБЮЊжїЬтЕФЦпФъМЖбЇЩњгаЖрЩйУћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌе§ЗНаЮABCDЕФЮЛжУШчЭМЫљЪОЃЌЕуAЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌЕуDЕФзјБъЮЊЃЈ0ЃЌ4ЃЉЃЎбгГЄCBНЛxжсгкЕуA1ЃЌзїе§ЗНаЮA1B1C1CЃЛбгГЄC1B1НЛxжсгкЕуA2ЃЌзїе§ЗНаЮA2B2C2C1ЁАДетбљЕФЙцТЩНјааЯТШЅЃЌЕк2018Иіе§ЗНаЮЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
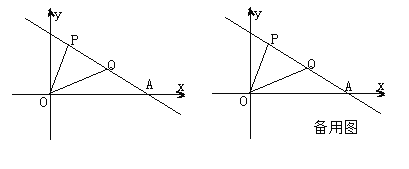
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§y=kx+bЕФЭМЯѓЙ§PЃЈ1ЃЌ4ЃЉЃЌQЃЈ4ЃЌ2ЃЉСНЕуЃЌЧвгыxжсНЛгкAЕуЃЎ
ЃЈ1ЃЉЧѓAЕузјБъЃЛ
ЃЈ2ЃЉвбжЊЕуMдкxжсЩЯЃЌШєЪЙMP+MQЕФжЕзюаЁЃЌЧѓЕуMЕФзјБъМАMP+MQЕФзюаЁжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌдкзјБъЦНУцФкЪЧЗёЛЙДцдквЛЕуNЃЌЪЙMЃЌNЃЌAЃЌQЫФЕуЧЁКУЙЙГЩЦНааЫФБпаЮЃЌШєДцдкЧыЧѓГіЕуNЕФзјБъЃЌШєВЛДцдкЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(1)НтЗНГЬЃК3x+5ЃНx+2ЧыАДЫљИјЕМгяЃЌЬюаДЭъећ.
НтЃКвЦЯюЃЌЕУ3x____ЃН2____ЃЌ(вРОнЃК_____).
КЯВЂЭЌРрЯюЃЌЕУ______ЃЌ
ЯЕЪ§ЛЏЮЊ1ЃЌЕУ_____ЃЌ(вРОнЃК______).
(2)НтЗНГЬЃК2(x+15)ЃН18Љ3(xЉ9).
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com