
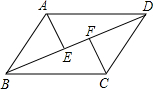
 如图,已知E、F在BD上,AE⊥BD于E,CF⊥BD于F,AD=BC,BE=DF,请问:△AED与△CFB全等吗?请说说明你的结论.
如图,已知E、F在BD上,AE⊥BD于E,CF⊥BD于F,AD=BC,BE=DF,请问:△AED与△CFB全等吗?请说说明你的结论. 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
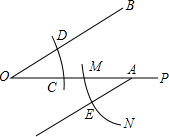 已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D,连接CD;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,连接ME,操作结果如图所示,下列结论不能由上述操作结果得出的是( )
已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D,连接CD;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,连接ME,操作结果如图所示,下列结论不能由上述操作结果得出的是( )| A、CD∥ME |
| B、OB∥AE |
| C、∠ODC=∠AEM |
| D、∠ACD=∠EAP |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,贴纸部分的面积为( )cm2.
如图,一扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,贴纸部分的面积为( )cm2.A、
| ||
B、
| ||
| C、800π | ||
| D、500π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com