
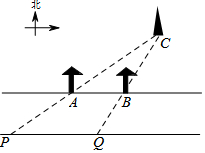
 如图,一条东西走向的笔直公路,点A、B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路PQ南侧直线行走,当他到达点P的位置时,观察树A恰好挡住电视塔,即点P、A、C在一条直线上,当他继续走180米到达点Q的位置时,以同样方法观察电视塔,观察树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧PQ的距离.
如图,一条东西走向的笔直公路,点A、B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路PQ南侧直线行走,当他到达点P的位置时,观察树A恰好挡住电视塔,即点P、A、C在一条直线上,当他继续走180米到达点Q的位置时,以同样方法观察电视塔,观察树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧PQ的距离. 分析 作CE⊥PQ交AB于D点,利用相似三角形对应边上的高的比等于相似比,即可求得电视塔到公路南侧所在直线的距离.
解答 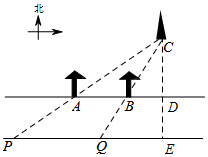 解:如图所示,作CE⊥PQ于E,交AB于D点,
解:如图所示,作CE⊥PQ于E,交AB于D点,
设CD为x,则CE=60+x,
∵AB∥PQ,
∴△ABC∽△PQC,
∴$\frac{CD}{AB}$=$\frac{CE}{PQ}$,即$\frac{x}{150}$=$\frac{x+60}{180}$,
解得x=300,
∴x+60=360米,
答:电视塔C到公路南侧所在直线PQ的距离是360米.
点评 本题考查了相似三角形的应用,解题的关键是正确的识别相似三角形.解题时注意:相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比等于相似比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连结DF并延长交AC于点E.若AB=8,BC=12,则线段EF的长为2.
如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连结DF并延长交AC于点E.若AB=8,BC=12,则线段EF的长为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
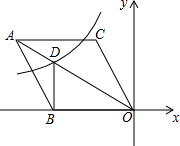 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,3$\sqrt{3}}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是-12$\sqrt{3}$.
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,3$\sqrt{3}}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是-12$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com