
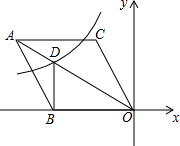
 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,3$\sqrt{3}}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是-12$\sqrt{3}$.
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,3$\sqrt{3}}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是-12$\sqrt{3}$. 分析 首先过点C作CE⊥x轴于点E,由顶点C的坐标为(-3,3$\sqrt{3}$),可求得OC的长,可得∠BOC=60°,又由菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,可求得OB的长,且∠AOB=30°,继而求得DB的长,则可求得点D的坐标,又由反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,即可求得答案.
解答 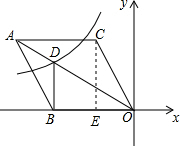 解:过点C作CE⊥x轴于点E,
解:过点C作CE⊥x轴于点E,
∵顶点C的坐标为(-3,3$\sqrt{3}$),
∴OE=3,CE=3$\sqrt{3}$,
∴∠BOC=60°,
∵四边形ABOC是菱形,
∴OB=OC=$\frac{CE}{sin60°}$=6,∠BOD=$\frac{1}{2}$∠BOC=30°,
∵DB⊥x轴,
∴DB=OB•tan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
∴点D的坐标为:(-6,2$\sqrt{3}$),
∵反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,
∴k=xy=-12$\sqrt{3}$.
故答案为:-12$\sqrt{3}$.
点评 此题考查了菱形的性质以及反比例函数图象上点的坐标特征.注意准确作出辅助线,求得点D的坐标是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
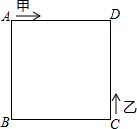 如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若甲的速度是乙的速度的3倍,则它们第2017次相遇在边CD上.
如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若甲的速度是乙的速度的3倍,则它们第2017次相遇在边CD上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧$\widehat{OB}$上一点,则∠ACB=( )
如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧$\widehat{OB}$上一点,则∠ACB=( )| A. | 80° | B. | 90° | C. | 100° | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
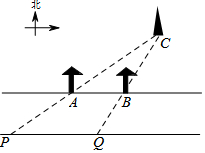 如图,一条东西走向的笔直公路,点A、B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路PQ南侧直线行走,当他到达点P的位置时,观察树A恰好挡住电视塔,即点P、A、C在一条直线上,当他继续走180米到达点Q的位置时,以同样方法观察电视塔,观察树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧PQ的距离.
如图,一条东西走向的笔直公路,点A、B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路PQ南侧直线行走,当他到达点P的位置时,观察树A恰好挡住电视塔,即点P、A、C在一条直线上,当他继续走180米到达点Q的位置时,以同样方法观察电视塔,观察树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧PQ的距离.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
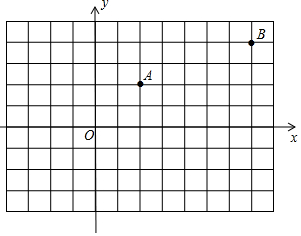 如图,已知A,B两村庄的坐标分别为(2,2),(7,4),一辆汽车从O点出发,在x轴上行驶.
如图,已知A,B两村庄的坐标分别为(2,2),(7,4),一辆汽车从O点出发,在x轴上行驶.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com