
| A. | 1:2:2$\sqrt{3}$ | B. | 1:2:$\sqrt{3}$ | C. | 3:2:1 | D. | 1:2:3 |
分析 连接OB,AO,延长AO交BC于D,根据⊙O是等边三角形ABC的外接圆求出∠OBC=30°,推出OB=2OD,求出AD=$\frac{3}{2}$OB,代入求出即可.
解答 解:连接OB,AO,延长AO交BC于D,
设正三角形的边长为a,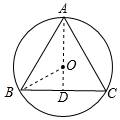
∵⊙O是等边三角形ABC的外接圆,
∴AD⊥BC,∠OBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,
∴BD=$\frac{1}{2}$a.
∵∠ADB=90°,∠OBC=30°,
∴OD=BD×tan30°=$\frac{\sqrt{3}}{6}$,OB=$\frac{\sqrt{3}}{3}$a,AD=AB•cos30°=$\frac{\sqrt{3}}{2}$a,
∴正三角形的高、外接圆半径、边心距之比=AD:OB:OD═3:2:1.,
故选:C.
点评 本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 不赚不赔 | B. | 赚了490元 | C. | 亏了450元 | D. | 亏了490元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象必经过点(-2,1) | B. | y随x的增大而增大 | ||
| C. | 当x>$\frac{1}{2}$时,y<0 | D. | 图象不经过第一象限 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:单选题
某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是 ( )
A. (3+x)(4﹣0.5x)=15 B. (x+3)(4+0.5x)=15
C. (x+4)(3﹣0.5x)=15 D. (x+1)(4﹣0.5x)=15
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com