

���� ��1����A��ֱ���ϣ�ȷ����ֱ�߽���ʽ������ȷ������B���ꣻ
��2����AP=OP��AP=OA��OP=OA��������г�����ȷ������P�����꣬�����ó�AP�������ʱ�䣻
��3�����ݵ��������ε����ʹ����ͼ�Σ��ó�OC'���õ��������ε����ߺ�һȷ������C�����꣬���������ʽ�У����ɵó�m��n��
��� �⣺��1����ֱ��y=$\frac{4}{3}$x+b�ֱ�y�ᡢx���ڵ�A��B����֪��A��0��4����
��b=4��
��ֱ��AB����ʽΪy=$\frac{4}{3}$x+4��
��B��-3��0����
��2���ɣ�1��֪��ֱ��AB����ʽΪy=$\frac{4}{3}$x+4��A��0��4����B��-3��0����
��P��m��$\frac{4}{3}$m+4����m��0����
��AP2=m2+$\frac{16}{9}$m2=$\frac{25}{9}$m2��OP2=m2+��$\frac{4}{3}$m+4��2=$\frac{25}{9}$m2+$\frac{32}{3}$m+16��OA2=25��
�ߡ�APOΪ���������Σ�
��ٵ�AP=AOʱ��
��AP2=AO2��
��$\frac{25}{9}$m2=25��
��m=5���ᣩ��m=-5��
��AP=5��
��t=AP��2=$\frac{5}{2}$��
�ڵ�AP=OPʱ��
��AP2=OP2��
��$\frac{25}{9}$m2=$\frac{25}{9}$m2+$\frac{32}{3}$m+16��
��m=-$\frac{3}{2}$��
��AP=$\frac{5}{3}$|m|=$\frac{5}{2}$��
��t=AP��2=$\frac{5}{4}$��
��OA=OPʱ��
��OA2=OP2��
��$\frac{25}{9}$m2+$\frac{32}{3}$m+16=25��
��m=$\frac{-48+3\sqrt{31}}{25}$��m=$\frac{-48-3\sqrt{31}}{25}$��
��AP=$\frac{5}{3}$|m|=$\frac{16-\sqrt{31}}{5}$��AP=$\frac{16+\sqrt{31}}{5}$��
��t=AP��2=$\frac{16-\sqrt{31}}{10}$��t=$\frac{16+\sqrt{31}}{10}$��
��������������t��ֵΪ$\frac{5}{2}$��$\frac{5}{4}$��$\frac{16-\sqrt{31}}{10}$��$\frac{16+\sqrt{31}}{10}$��
��3����ͼ�� �ɣ�2��֪��AB=5����OB���ӳ�����ȡһ��C��ʹBC=AB=5��
�ɣ�2��֪��AB=5����OB���ӳ�����ȡһ��C��ʹBC=AB=5��
��OB=3��
��OC=8��
��BC=AB��
���ABO=2��AC'O��
�ߡ�ABC=2��ACB��
���AC'O=��ACB��
��OA��CC'��
��OC=OC'=8��
��C��8��0����
��A��0��4����
�ཫA��C�������y=mx+n�ã�$\left\{\begin{array}{l}{n=4}\\{8m+4=0}\end{array}\right.$��
��$\left\{\begin{array}{l}{m=-\frac{1}{2}}\\{n=4}\end{array}\right.$��
�ʴ�Ϊ��-$\frac{1}{2}$��4��
���� ������һ�κ����ۺ��⣬��Ҫ�����˴���ϵ���������������ε����ʣ��Ȿ��Ĺؼ����г����̣��÷��̵�˼���ǽ������Ŀ���õķ�����


 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x-7 | B�� | 2x-1=$\frac{1}{x}$ | C�� | 4x-3=21x+17 | D�� | x2-3=x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
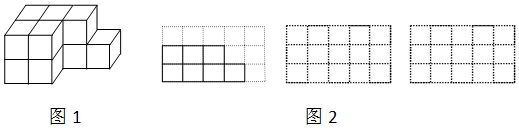
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
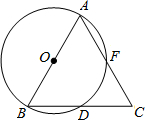 ��ͼ��AB�ǡ�O��ֱ����BD�ǡ�O���ң��ӳ�BD����C��ʹDC=BD������AC����O�ڵ�F��
��ͼ��AB�ǡ�O��ֱ����BD�ǡ�O���ң��ӳ�BD����C��ʹDC=BD������AC����O�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
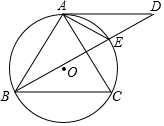 ��ͼ����OΪABC�����Բ��ADΪ��O�����ߣ�AD��BC��BD����O��E���ҵ�E��$\widehat{AC}$���е㣬����AE��
��ͼ����OΪABC�����Բ��ADΪ��O�����ߣ�AD��BC��BD����O��E���ҵ�E��$\widehat{AC}$���е㣬����AE���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com