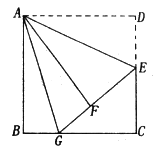
【题目】已知：如图，在边长为8的正方形ABCD中，E是边CD的中点，将
沿AE对折至
，延长EF交边BC于点G，连接AG。
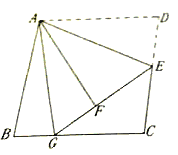
（1）求证：
； （2）求BG的长。
【答案】（1）、证明过程见解析；（2）、
【解析】
试题分析：（1）、根据折叠图形的性质得出AD=AF，BE=EF，∠D＝∠AFE＝90°，从而得出AB=AF，∠B＝∠AFG＝90°，结合AG为公共边，利用HL判定定理得出三角形全等；（2）、设BG=FG=x，则GC=8-x，根据中点的性质得出EG=4+x，根据Rt△CEG的勾股定理求出x的值，得出答案.
试题解析：（1）、在正方形ABCD中，
，∠D＝∠B＝∠BCD＝90°
∵将△ADE沿AE对折至△AFE， 
，∠D＝∠AFE＝90°，
，∠B＝∠AFG＝90° 又
， ∴△ABG≌△AFG（HL）
（2）、∵△ABG≌△AFG，
， 设
，则
，
∵E为CD的中点，
，
∴在Rt△CEG中，
，解得
， 
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案科目：初中数学 来源： 题型：
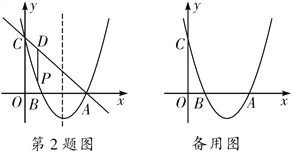
【题目】如图，抛物线y＝x2＋bx＋c过点A(3，0)，B(1，0)，交y轴于点C，点P是该抛物线上一动点，点P从C点沿抛物线向A点运动(点P不与点A重合)，过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式；
(2)求点P在运动的过程中线段PD长度的最大值；
(3)在抛物线对称轴上是否存在点M，使|MA－MC|最大？若存在，请求出点M的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形OABC在平面直角坐标系内（O为坐标原点），点A在x轴上，点C在y轴上，点B的坐标为（﹣4，﹣4
），点E是BC的中点，现将矩形折叠，折痕为EF，点F为折痕与y轴的交点，EF交x轴于G且使∠CEF=60°．
（1）求证：△EFC≌△GFO；
（2）求点D的坐标；
（3）若点P（x，y）是线段EG上的一点，设△PAF的面积为s，求s与x的函数关系式并写出x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年某市约有108000名应届初中毕业生参加中考，按四舍五入保留两位有效数字，108000用科学计数法表示为( )
(A)0.10×106 (B)1.08×105 (C)0.11×106 (D)1.1×105
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC=2，∠BAC=20°．动点P、Q分别在直线BC上运动，且始终保持∠PAQ=100°．设BP=x，CQ=y，则y与x之间的函数关系用图象大致可以表示为（ ）
A．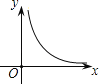 
B． 
C． 
D． 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com