
【题目】某商场试销一种成本为![]() 元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于
元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)符合一次函数
(元/件)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)写出销售单价![]() 的取值范围;
的取值范围;
(2)求出一次函数![]() 的解析式;
的解析式;
(3)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
【答案】(1)60≤x≤84;(2)y=﹣x+120;(3)当销售价定为84元/件时,最大利润是864元.
【解析】
(1)根据“规定试销期间单价不低于成本单价,又获利不得高于40%”写出x的取值范围便可;
(2)可用待定系数法来确定一次函数的解析式;
(3)根据利润=销售量×单件的利润,然后将(2)中的函数式代入其中,求出利润和销售单件之间的关系式,然后根据其性质来判断出最大利润.
解:(1)根据题意得,
60≤x≤60×(1+40%),
即60≤x≤84;
(2)由题意得:![]() ,
,
∴![]() .
.
∴一次函数的解析式为:y=﹣x+120;
(3)w=(x﹣60)(﹣x+120)=﹣x2+180x﹣7200=﹣(x﹣90)2+900,
∵抛物线开口向下,
∴当x<90时,w随x的增大而增大,
而60≤x≤84,
∴当x=84时,w=(84﹣60)×(120﹣84)=864.
答:当销售价定为84元/件时,商场可以获得最大利润,最大利润是864元.


科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径的弧经过点
为半径的弧经过点![]() 是弧
是弧![]() 上一个动点.
上一个动点.
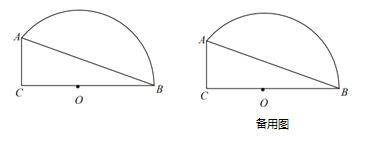
![]() 求半径
求半径![]() 的长;
的长;
![]() 如果点
如果点![]() 是弧
是弧![]() 的中点,联结
的中点,联结![]() ,求
,求![]() 的正切值;
的正切值;
![]() 如果
如果![]() 平分
平分![]() ,延长
,延长![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,抛物线y=﹣![]() x2+x+4与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
x2+x+4与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
(1)求直线BD的解析式;
(2)如图②,点P是直线BE上方抛物线上一动点,连接PD,PF,当△PDF的面积最大时,在线段BE上找一点G,使得PG﹣![]() GE的值最小,求出点G的坐标及PG﹣
GE的值最小,求出点G的坐标及PG﹣![]() GE的最小值;
GE的最小值;
(3)将抛物线沿直线AC平移,点A,C平移后的对应点为A′,C'.在平面内有一动点H,当以点B,A',C',H为顶点的四边形为平行四边形时,在直线AC上方找一个满足条件的点H,与直线AC下方所有满足条件的点H为顶点的多边形为轴对称图形时,求出点A′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)求抛物线的解析式;
(2)若动点P在第四象限内的抛物线上,过动点P作x轴的垂线交直线AC于点D,交x轴于点E,垂足为E,求线段PD的长,当线段PD最长时,求出点P的坐标;
(3)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=AC,E是边BC上的点,且∠AED=∠CAD,DE交AC于点F.
(1)求证:△ABE∽△DAF;
(2)当ACFC=AEEC时,求证:AD=BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
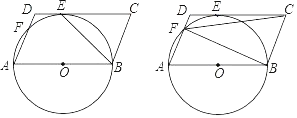
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD切于点E,AD交⊙O于点F.
(1)求证:∠ABE=45°;
(2)连接CF,若CE=2DE,求tan∠DFC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
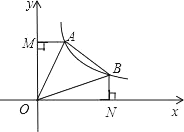
【题目】如图,直线y=﹣x+b与双曲线![]() 交于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,有以下结论:①S△AOM=S△BON;②OA=OB;③五边形MABNO的面积
交于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,有以下结论:①S△AOM=S△BON;②OA=OB;③五边形MABNO的面积![]() ;④若∠AOB=45°,则S△AOB=2k,⑤当AB=
;④若∠AOB=45°,则S△AOB=2k,⑤当AB=![]() 时,ON﹣BN=1;其中结论正确的个数有( )
时,ON﹣BN=1;其中结论正确的个数有( )
A. 5个B. 4个C. 3个D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com