
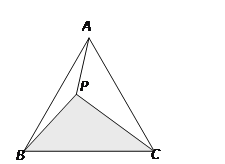
【题目】如图,已知P为等边△ABC形内一点,且PA=3cm,PB=4 cm,PC=5 cm,则图中△PBC的面积为________cm2.
【答案】4![]() +3
+3
【解析】
将△BPC绕点B逆时针旋转60°得到△BKA,可得△KBP为等边三角形,KP=4,因为AP2+KP2=AK2,可得∠APK=90°,所以∠APB=150°,作BH⊥AP于H,则∠BPH=30°,根据△PBC的面积=△AKB的面积=S△APK+S△BPK-S△APB即可得出△PBC的面积.
解:如图,将△BPC绕点B逆时针旋转60°得到△BKA,
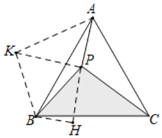
则PB=BK=4,AK=PC=5,∠PBK=60°,
∴△KBP为等边三角形,
∴∠KPB=60°,KP=4,
∵AP=3,
∴AP2+KP2=AK2,
∴∠APK=90°,
∴∠APB=150°,
作BH⊥AP于H,则∠BPH=30°,
∴BH=![]() BP=2,
BP=2,
∴△PBC的面积=△AKB的面积=S△APK+S△BPK-S△APB=![]() ×3×4+
×3×4+![]() ×42
×42![]() ×2×3=3+4
×2×3=3+4![]() .
.
故答案为:4![]() +3.
+3.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知二次函数y=ax2﹣2ax﹣3a(a>0)图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为D.
(1)求点A,B的坐标;
(2)若M为对称轴与x轴交点,且DM=2AM.
①求二次函数解析式;
②当t﹣2≤x≤t时,二次函数有最大值5,求t值;
③若直线x=4与此抛物线交于点E,将抛物线在C,E之间的部分记为图象记为图象P(含C,E两点),将图象P沿直线x=4翻折,得到图象Q,又过点(10,﹣4)的直线y=kx+b与图象P,图象Q都相交,且只有两个交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若cosC=![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
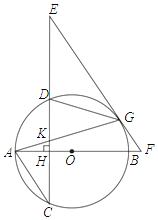
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,高新区凌水河治理工程正式启动,若由甲工程队单独完成需10个月;若由甲、乙两工程队合做4个月后,剩下工程由乙工程队再做5个月可以完成。(1)乙工程队单独完成这项工程需几个月的时间?
(2)已知甲工程队每月施工费用为15万元,比乙工程队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲、乙工程队同时开工,甲工程队做![]() 个月,乙工程队做
个月,乙工程队做![]() 个月(
个月(![]() 均为整数)分工合作的方式施工,问有哪几种施工方案?
均为整数)分工合作的方式施工,问有哪几种施工方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
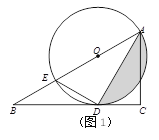
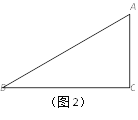
【题目】如图,在Rt△ABC中,∠C=90°,O为斜边AB上一点,以O为圆心、OA为半径的圆恰好与BC相切于点D,与AB的另一个交点为E,连接DE.
(1)请找出图中与△ADE相似的三角形,并说明理由;
(2)若AC=3,AE=4,试求图中阴影部分的面积;
(3)小明在解题过程中思考这样一个问题:如图中的⊙O的圆心究竟是怎么确定的呢?请你在如图中利用直尺和圆规找到符合题意的圆心O,并写出你的作图方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
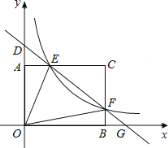
【题目】如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B.C重合),过点F的反比例函数y=![]() 的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为
的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为![]() ;②若k=
;②若k=![]() ,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=
,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=![]() ,则k=1.其中正确的命题的序号是____________(填序号).
,则k=1.其中正确的命题的序号是____________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了安全,交通部门一再提醒司机:请勿超速!同时,进一步完善各类监测系统,如图,在松铜公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了测速点C,从测速点C测得一小车从点A到达点B行驶了3秒钟,已知∠CAN=45°,∠CBN=60°,BC=120米.
(1)求测速点C到该段公路的距离;
(2)请你通过计算判断此车是否超速,(结果精确到0.1m/s)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为![]() 元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于
元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)符合一次函数
(元/件)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)写出销售单价![]() 的取值范围;
的取值范围;
(2)求出一次函数![]() 的解析式;
的解析式;
(3)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com