
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若cosC=![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
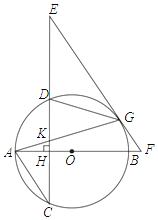
【答案】(1)详见解析;(2)①详见解析;②![]() .
.
【解析】
(1)连接OG,由EG=EK知∠KGE=∠GKE=∠AKH,结合OA=OG知∠OGA=∠OAG,根据CD⊥AB得∠AKH+∠OAG=90°,从而得出∠KGE+∠OGA=90°,据此即可得证;
(2)①由AC∥EF知∠E=∠C=∠AGD,结合∠DKG=∠GKE即可证得△KGD∽△KEG;
②连接OG,由![]() 设CH=4k,AC=5k,可得AH=3k,CK=AC=5k,HK=CK-CH=k.利用AH2+HK2=AK2得k=1,即可知CH=4,AC=5,AH=3,再设⊙O半径为R,由OH2+CH2=OC2可求得
设CH=4k,AC=5k,可得AH=3k,CK=AC=5k,HK=CK-CH=k.利用AH2+HK2=AK2得k=1,即可知CH=4,AC=5,AH=3,再设⊙O半径为R,由OH2+CH2=OC2可求得![]() ,根据
,根据![]() 知
知![]() ,从而得出答案.
,从而得出答案.
解:(1)如图,连接OG.
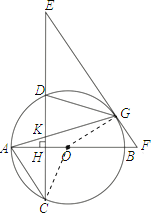
∵EG=EK,
∴∠KGE=∠GKE=∠AKH,
又OA=OG,
∴∠OGA=∠OAG,
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
∴∠KGE+∠OGA=90°,
∴EF是⊙O的切线.
(2)①∵AC∥EF,
∴∠E=∠C,
又∠C=∠AGD,
∴∠E=∠AGD,
又∠DKG=∠GKE,
∴△KGD∽△KEG;
②连接OG,
∵![]() ,AK=
,AK=![]() ,
,
设![]() ,
,
∴设CH=4k,AC=5k,则AH=3k
∵KE=GE,AC∥EF,
∴CK=AC=5k,
∴HK=CK-CH=k.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即![]() ,
,
解得k=1,
∴CH=4,AC=5,则AH=3,
设⊙O半径为R,在Rt△OCH中,OC=R,OH=R-3,CH=4 ,
由勾股定理得:OH2+CH2=OC2,即(R-3)2+42=R2,
∴![]() ,
,
在Rt△OGF中,![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为:(1)详见解析;(2)①详见解析;②![]()


科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,则巡逻船从出发到成功拦截捕鱼船所用的时间是( )

A. 1小时 B. 2小时 C. 3小时 D. 4小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
![]()
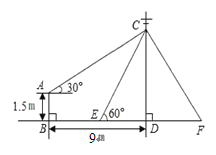
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A是双曲线![]() (k1>0)上一点,点A的横坐标为1,过点A作平行于y轴的直线,与x轴交于点B,与双曲线
(k1>0)上一点,点A的横坐标为1,过点A作平行于y轴的直线,与x轴交于点B,与双曲线![]() (k2<0)交于点C.点D(m,0)是x轴上一点,且位于直线AC右侧,E是AD的中点.
(k2<0)交于点C.点D(m,0)是x轴上一点,且位于直线AC右侧,E是AD的中点.
(1)当m=4时,求△ACD的面积(用含k1、k2的代数式表示);
(2)若点E恰好在双曲线![]() (k1>0)上,求m的值;
(k1>0)上,求m的值;
(3)设线段EB的延长线与y轴的负半轴交于点F,当点D的坐标为D(2,0)时,若△BDF的面积为1,且CF∥AD,求k1的值,并直接写出线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)请用列表法或树状图写出所有的等可能性结果,写出所有个位数字是6的“两位递增数”;
(2)求抽取的“两位递增数”的个位数字与十位数字之积能被5整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
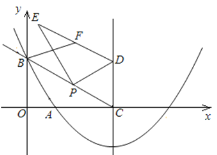
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 过点
过点![]() ,
,![]() ,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且CPD=
,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且CPD=![]() .
.
(1)求抛物线的函数表达式;
(2)若点P的横坐标为m,△PCD的面积为S,求S与m之间的函数关系式;
(3)过点P作PE⊥DP,连接DE,F为DE的中点,试求线段BF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径的弧经过点
为半径的弧经过点![]() 是弧
是弧![]() 上一个动点.
上一个动点.
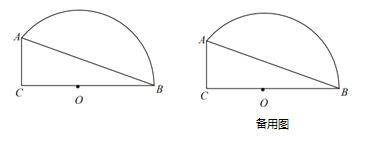
![]() 求半径
求半径![]() 的长;
的长;
![]() 如果点
如果点![]() 是弧
是弧![]() 的中点,联结
的中点,联结![]() ,求
,求![]() 的正切值;
的正切值;
![]() 如果
如果![]() 平分
平分![]() ,延长
,延长![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com