
ЁОЬтФПЁПвбжЊЕуAЪЧЫЋЧњЯп![]() ЃЈk1ЃО0ЃЉЩЯвЛЕуЃЌЕуAЕФКсзјБъЮЊ1ЃЌЙ§ЕуAзїЦНаагкyжсЕФжБЯпЃЌгыxжсНЛгкЕуBЃЌгыЫЋЧњЯп
ЃЈk1ЃО0ЃЉЩЯвЛЕуЃЌЕуAЕФКсзјБъЮЊ1ЃЌЙ§ЕуAзїЦНаагкyжсЕФжБЯпЃЌгыxжсНЛгкЕуBЃЌгыЫЋЧњЯп![]() ЃЈk2ЃМ0ЃЉНЛгкЕуCЃЎЕуDЃЈmЃЌ0ЃЉЪЧxжсЩЯвЛЕуЃЌЧвЮЛгкжБЯпACгвВрЃЌEЪЧADЕФжаЕуЃЎ
ЃЈk2ЃМ0ЃЉНЛгкЕуCЃЎЕуDЃЈmЃЌ0ЃЉЪЧxжсЩЯвЛЕуЃЌЧвЮЛгкжБЯпACгвВрЃЌEЪЧADЕФжаЕуЃЎ
ЃЈ1ЃЉЕБmЃН4ЪБЃЌЧѓЁїACDЕФУцЛ§ЃЈгУКЌk1ЁЂk2ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉШєЕуEЧЁКУдкЫЋЧњЯп![]() ЃЈk1ЃО0ЃЉЩЯЃЌЧѓmЕФжЕЃЛ
ЃЈk1ЃО0ЃЉЩЯЃЌЧѓmЕФжЕЃЛ
ЃЈ3ЃЉЩшЯпЖЮEBЕФбгГЄЯпгыyжсЕФИКАыжсНЛгкЕуFЃЌЕБЕуDЕФзјБъЮЊDЃЈ2ЃЌ0ЃЉЪБЃЌШєЁїBDFЕФУцЛ§ЮЊ1ЃЌЧвCFЁЮADЃЌЧѓk1ЕФжЕЃЌВЂжБНгаДГіЯпЖЮCFЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЌ
ЃЌ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩгкAЁЂCЕФКсзјБъЯрЭЌЃЌдђACЕФГЄМДЮЊAЁЂCЕФзнзјБъжЎВюЃЌИљОнm=4ЃЌПЩЧѓГіBDЕФГЄЃЌНјЖјЕФЕУГіШ§НЧаЮЕФУцЛ§ЃЛ
ЃЈ2ЃЉзїEGЁЭxжсгкЕуGЃЌХаЖЯГіЁїDEGЁзЁїDABЃЌдйИљОнAЃЌBЃЌDШ§ЕуЕФзјБъЗжБ№ЮЊAЃЈ1ЃЌk1ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌDЃЈmЃЌ0ЃЉЃЌвдМАGЮЊBDЕФжаЕуЃЌЧѓГіEЕФБэДяЪНЃЌДњШыЗДБШР§КЏЪ§НтЮіЪНЃЌМДПЩЧѓГіmЕФжЕЃЛ
ЃЈ3ЃЉИљОнSЁїBDF=1ЃЌЧѓГіOF=2ЃЌНЋЕуBЃЌЕуEЕФзјБъЗжБ№ДњШыНтЮіЪНЃЌЧѓГіжБЯпBEЕФНтЮіЪНЮЊy=k1x-k1ЃЎдйЧѓГіADЕФНтЮіЪНЃЌИљОнЦНаажБЯпЕФаджЪЧѓГіFCЕФНтЮіЪНЃЌЕУЕНCЕузјБъЃЌДгЖјЧѓГіFЕуЕФзјБъЃЎ
ЃЈ1ЃЉгЩЬтвтЕУAЃЌCСНЕуЕФзјБъЗжБ№ЮЊAЃЈ1ЃЌk1ЃЉЃЌCЃЈ1ЃЌk2ЃЉЃЎЃЈШчЭМ1ЃЉ
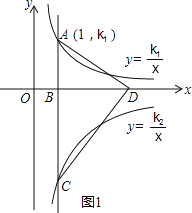
Ёпk1ЃО0ЃЌk2ЃМ0ЃЌ
ЁрЕуAдкЕквЛЯѓЯоЃЌЕуCдкЕкЫФЯѓЯоЃЌAC=k1-k2ЃЎ
ЕБm=4ЪБЃЌSЁїACDЃН![]() ACBDЃН
ACBDЃН![]() (k1k2)ЃЎ
(k1k2)ЃЎ
ЃЈ2ЃЉзїEGЁЭxжсгкЕуGЃЎЃЈШчЭМ2ЃЉ
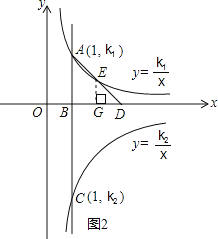
ЁпEGЁЮABЃЌADЕФжаЕуЮЊEЃЌ
ЁрЁїDEGЁзЁїDABЃЌ![]() ЃЌGЮЊBDЕФжаЕуЃЎ
ЃЌGЮЊBDЕФжаЕуЃЎ
ЁпAЃЌBЃЌDШ§ЕуЕФзјБъЗжБ№ЮЊAЃЈ1ЃЌk1ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌDЃЈmЃЌ0ЃЉЃЌ
ЁрEGЃН![]() ЃЌBGЃН
ЃЌBGЃН![]() ЃЌOGЃНOB+BGЃН
ЃЌOGЃНOB+BGЃН![]() ЃЎ
ЃЎ
ЁрЕуEЕФзјБъЮЊE(![]() ЃЌ
ЃЌ![]() )ЃЎ
)ЃЎ
ЁпЕуEЧЁКУдкЫЋЧњЯпyЃН![]() ЩЯЃЌ
ЩЯЃЌ
Ёр![]()
![]() ЃНk1ЃЎЂй
ЃНk1ЃЎЂй
Ёпk1ЃО0ЃЌ
ЁрЗНГЬЂйПЩЛЏЮЊ![]() ЃН1ЃЌ
ЃН1ЃЌ
НтЕУm=3ЃЎ
ЃЈ3ЃЉЕБЕуDЕФзјБъЮЊDЃЈ2ЃЌ0ЃЉЪБЃЌгЩЃЈ2ЃЉПЩжЊЕуEЕФзјБъЮЊE(![]() ЃЌ
ЃЌ![]() )ЃЎЃЈШчЭМ3ЃЉ
)ЃЎЃЈШчЭМ3ЃЉ
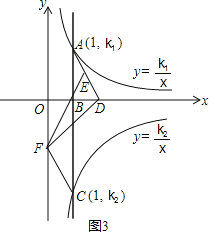
ЁпSЁїBDF=1ЃЌ
ЁрSЁїBDFЃН![]() BDOFЃН
BDOFЃН![]() OFЃН1ЃЎ
OFЃН1ЃЎ
ЁрOF=2ЃЎ
ЩшжБЯпBEЕФНтЮіЪНЮЊy=ax+bЃЈaЁй0ЃЉЃЎ
ЁпЕуBЃЌЕуEЕФзјБъЗжБ№ЮЊBЃЈ1ЃЌ0ЃЉЃЌE(![]() ЃЌ
ЃЌ![]() )ЃЌ
)ЃЌ
Ёр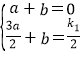
НтЕУa=k1ЃЌb=-k1ЃЎ
ЁржБЯпBEЕФНтЮіЪНЮЊy=k1x-k1ЃЎ
ЁпЯпЖЮEBЕФбгГЄЯпгыyжсЕФИКАыжсНЛгкЕуFЃЌk1ЃО0ЃЌ
ЁрЕуFЕФзјБъЮЊFЃЈ0ЃЌ-k1ЃЉЃЌOF=k1ЃЎ
Ёрk1=2ЃЎ
ЁпAЕузјБъЮЊЃЈ1ЃЌ2ЃЉЃЌDЕузјБъЮЊЃЈ2ЃЌ0ЃЉЃЌ
ЁрЩшвЛДЮКЏЪ§НтЮіЪНЮЊy=kx+bЃЌ
НЋAЃЈ1ЃЌ2ЃЉЃЌDЃЈ2ЃЌ0ЃЉЗжБ№ДњШыНтЮіЪНЕУЃЌ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЙЪКЏЪ§НтЮіЪНЮЊy=-2x+4ЃЌ
гжЁпADЁЮFCЃЌ
ЩшFCЕФНтЮіЪНЮЊy=-2x+cЃЌ
НЋFЃЈ0ЃЌ-2ЃЉДњШыНтЮіЪНЕУЃЌc=-2ЃЌ
ЙЪКЏЪ§НтЮіЪНЮЊy=-2x-2ЃЎ
ЕБx=1ЪБЃЌk2=-4ЃЎ
CЕузјБъЮЊЃЈ1ЃЌ-4ЃЉЃЌ
ЙЪЯпЖЮCF=![]() ЃЎ
ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЁЂ
ЁЂ![]() НЛгкЕу
НЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() ЕФЯпЖЮ
ЕФЯпЖЮ![]() гы
гы![]() ЁЂ
ЁЂ![]() ЗжБ№НЛгкЕу
ЗжБ№НЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЌШчЙћ
ЃЌШчЙћ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌФЧУДЫФБпаЮ
ЃЌФЧУДЫФБпаЮ![]() ЕФжмГЄЮЊ__ЃЎ
ЕФжмГЄЮЊ__ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
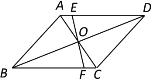
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЖўДЮКЏЪ§y=ax2Љ2axЉ3aЃЈaЃО0ЃЉЭМЯѓгыxжсНЛгкЕуAЃЌBЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌЖЅЕуЮЊDЃЎ
ЃЈ1ЃЉЧѓЕуAЃЌBЕФзјБъЃЛ
ЃЈ2ЃЉШєMЮЊЖдГЦжсгыxжсНЛЕуЃЌЧвDM=2AMЃЎ
ЂйЧѓЖўДЮКЏЪ§НтЮіЪНЃЛ
ЂкЕБtЉ2ЁмxЁмtЪБЃЌЖўДЮКЏЪ§газюДѓжЕ5ЃЌЧѓtжЕЃЛ
ЂлШєжБЯпx=4гыДЫХзЮяЯпНЛгкЕуEЃЌНЋХзЮяЯпдкCЃЌEжЎМфЕФВПЗжМЧЮЊЭМЯѓМЧЮЊЭМЯѓPЃЈКЌCЃЌEСНЕуЃЉЃЌНЋЭМЯѓPбижБЯпx=4ЗелЃЌЕУЕНЭМЯѓQЃЌгжЙ§ЕуЃЈ10ЃЌЉ4ЃЉЕФжБЯпy=kx+bгыЭМЯѓPЃЌЭМЯѓQЖМЯрНЛЃЌЧвжЛгаСНИіНЛЕуЃЌЧѓbЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
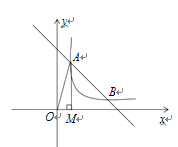
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНЃxЃЋ6ЕФЭМЯёгыЗДБШР§КЏЪ§yЃН![]() (k>0)ЕФЭМЯёНЛгкAЁЂBСНЕуЃЌЙ§AЕузїxжсЕФДЙЯпЃЌДЙзуЮЊMЃЌЁїAOMЕФУцЛ§ЮЊ2.5.
(k>0)ЕФЭМЯёНЛгкAЁЂBСНЕуЃЌЙ§AЕузїxжсЕФДЙЯпЃЌДЙзуЮЊMЃЌЁїAOMЕФУцЛ§ЮЊ2.5.
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкyжсЩЯгавЛЕуPЃЌЕБPAЃЋPBЕФжЕзюаЁЪБЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуOдкЁїABCФкЃЌЕуPЁЂQЁЂRЗжБ№дкБпABЁЂBCЁЂCAЩЯЃЌЧвOPЁЮBCЃЌOQЁЮCAЃЌORЁЮABЃЌOP=OQ=OR=xЃЌBC=aЃЌCA=bЃЌAB=cЃЌдђx=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
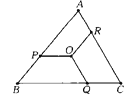
ЁОЬтФПЁПШчЭМЃЌвбжЊEЃЌFЗжБ№ЮЊе§ЗНаЮABCDЕФБпABЃЌBCЕФжаЕуЃЌAFгыDEНЛгкЕуMЃЌOЮЊBDЕФжаЕуЃЌдђЯТСаНсТлЃК
ЂйЁЯAME=90ЁуЃЛЂкЁЯBAF=ЁЯEDBЃЛЂлЁЯBMO=90ЁуЃЛЂмMD=2AM=4EMЃЛЂнAM=![]() MFЃЎЦфжае§ШЗНсТлЕФЪЧЃЈЁЁЁЁЃЉ
MFЃЎЦфжае§ШЗНсТлЕФЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂлЂм B. ЂкЂмЂн C. ЂйЂлЂмЂн D. ЂйЂлЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвCDЁЭABгкHЃЌGЮЊЁбOЩЯвЛЕуЃЌСЌНгAGНЛCDгкKЃЌдкCDЕФбгГЄЯпЩЯШЁвЛЕуEЃЌЪЙEG=EKЃЌEGЕФбгГЄЯпНЛABЕФбгГЄЯпгкFЃЎ
ЃЈ1ЃЉЧѓжЄЃКEFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉСЌНгDGЃЌШєACЁЮEFЪБЃЎ
ЂйЧѓжЄЃКЁїKGDЁзЁїKEGЃЛ
ЂкШєcosC=![]() ЃЌAK=
ЃЌAK=![]() ЃЌЧѓBFЕФГЄЃЎ
ЃЌЧѓBFЕФГЄЃЎ
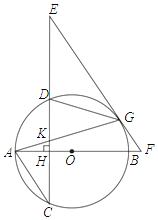
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАТЬЫЎЧрЩНОЭЪЧН№ЩНвјЩНЁБЃЌИпаТЧјСшЫЎКгжЮРэЙЄГЬе§ЪНЦєЖЏ,ШєгЩМзЙЄГЬЖгЕЅЖРЭъГЩаш10ИідТЃЛШєгЩМзЁЂввСНЙЄГЬЖгКЯзі4ИідТКѓ,ЪЃЯТЙЄГЬгЩввЙЄГЬЖгдйзі5ИідТПЩвдЭъГЩЁЃ(1)ввЙЄГЬЖгЕЅЖРЭъГЩетЯюЙЄГЬашМИИідТЕФЪБМфЃП
(2)вбжЊМзЙЄГЬЖгУПдТЪЉЙЄЗбгУЮЊ15ЭђдЊ,БШввЙЄГЬЖгЖр6ЭђдЊ,АДвЊЧѓИУЙЄГЬзмЗбгУВЛГЌЙ§141ЭђдЊ,ЙЄГЬБиаыдквЛФъФкПЂЙЄ(АќРЈ12ИідТ).ЮЊСЫШЗБЃОЗбКЭЙЄЦк,ВЩШЁМзЁЂввЙЄГЬЖгЭЌЪБПЊЙЄ,МзЙЄГЬЖгзі![]() ИідТ,ввЙЄГЬЖгзі
ИідТ,ввЙЄГЬЖгзі![]() ИідТ(
ИідТ(![]() ОљЮЊећЪ§)ЗжЙЄКЯзїЕФЗНЪНЪЉЙЄ,ЮЪгаФФМИжжЪЉЙЄЗНАИЃП
ОљЮЊећЪ§)ЗжЙЄКЯзїЕФЗНЪНЪЉЙЄ,ЮЪгаФФМИжжЪЉЙЄЗНАИЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫАВШЋЃЌНЛЭЈВПУХвЛдйЬсабЫОЛњЃКЧыЮ№ГЌЫйЃЁЭЌЪБЃЌНјвЛВНЭъЩЦИїРрМрВтЯЕЭГЃЌШчЭМЃЌдкЫЩЭЙЋТЗФГжБЯпТЗЖЮMNФкЯоЫй60ЧЇУз/аЁЪБЃЌЮЊСЫМьВтГЕСОЪЧЗёГЌЫйЃЌдкЙЋТЗMNХдЩшСЂСЫВтЫйЕуCЃЌДгВтЫйЕуCВтЕУвЛаЁГЕДгЕуAЕНДяЕуBааЪЛСЫ3УыжгЃЌвбжЊЁЯCANЃН45ЁуЃЌЁЯCBNЃН60ЁуЃЌBCЃН120УзЃЎ
ЃЈ1ЃЉЧѓВтЫйЕуCЕНИУЖЮЙЋТЗЕФОрРыЃЛ
ЃЈ2ЃЉЧыФуЭЈЙ§МЦЫуХаЖЯДЫГЕЪЧЗёГЌЫйЃЌЃЈНсЙћОЋШЗЕН0.1m/sЃЉЃЈВЮПМЪ§ОнЃК![]() Ёж1.41ЃЌ
Ёж1.41ЃЌ![]() Ёж1.73ЃЉ
Ёж1.73ЃЉ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com