
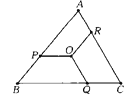
【题目】如图,点O在△ABC内,点P、Q、R分别在边AB、BC、CA上,且OP∥BC,OQ∥CA,OR∥AB,OP=OQ=OR=x,BC=a,CA=b,AB=c,则x=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
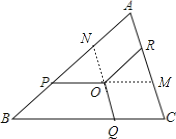
延长PO交AC于M,延长QO交AB于N,如图,设OP=OQ=OR=x,易证得四边形ANOR、四边形CMOQ为平行四边形,则MC=OQ=x,ON=AR,根据相似三角形的判定易得△ROM∽△ABC,利用相似比可得RM=![]() x,再判断△NOP∽△ACB,利用相似比可得NO=
x,再判断△NOP∽△ACB,利用相似比可得NO=![]() x,则AR=
x,则AR=![]() x,所以
x,所以![]() x+
x+![]() x+x=b,于是解得x=
x+x=b,于是解得x=![]() =
=![]() .
.
延长PO交AC于M,延长QO交AB于N,如图,
设OP=OQ=OR=x,
∵OP∥BC,OQ∥CA,OR∥AB,
∴四边形ANOR、四边形CMOQ为平行四边形,
∴MC=OQ=x,ON=AR,
易证得△ROM∽△ABC,
∴![]() ,即
,即![]() ,
,
∴RM=![]() x,
x,
易证得△NOP∽△ACB,
∴![]() ,即
,即![]() ,
,
∴NO=![]() x,
x,
∴AR=![]() x,
x,
∵AR+RM+MC=AC,
即![]() x+
x+![]() x+x=b,
x+x=b,
∴x=![]() =
=![]() ,
,
即OP的长为![]() .
.
故选A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了解全区5000名初中毕业生的体重情况,随机抽测了200名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为___人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() 和点
和点![]() 两点.
两点.
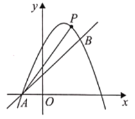
(1)求抛物线的函数表达式;
(2)若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,当
上方抛物线上的一动点,当![]() 的面积
的面积![]() 最大时,求此时
最大时,求此时![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,直接写出
是等腰三角形?若存在,直接写出![]() 点的坐标(不用说理);若不存在,请说明理由.
点的坐标(不用说理);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
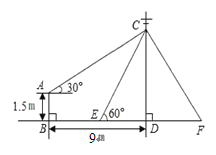
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
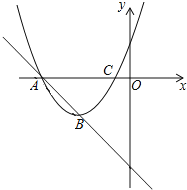
【题目】如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于A、B两个不同的点,其中点A在x轴上.
(1)n=3m-9(用含m的代数式表示);
(2)若点B为该抛物线的顶点,求m、n的值;
(3)①设m=-2,当-3≤x≤0时,求二次函数y=x2+mx+n的最小值;
②若-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A是双曲线![]() (k1>0)上一点,点A的横坐标为1,过点A作平行于y轴的直线,与x轴交于点B,与双曲线
(k1>0)上一点,点A的横坐标为1,过点A作平行于y轴的直线,与x轴交于点B,与双曲线![]() (k2<0)交于点C.点D(m,0)是x轴上一点,且位于直线AC右侧,E是AD的中点.
(k2<0)交于点C.点D(m,0)是x轴上一点,且位于直线AC右侧,E是AD的中点.
(1)当m=4时,求△ACD的面积(用含k1、k2的代数式表示);
(2)若点E恰好在双曲线![]() (k1>0)上,求m的值;
(k1>0)上,求m的值;
(3)设线段EB的延长线与y轴的负半轴交于点F,当点D的坐标为D(2,0)时,若△BDF的面积为1,且CF∥AD,求k1的值,并直接写出线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)请用列表法或树状图写出所有的等可能性结果,写出所有个位数字是6的“两位递增数”;
(2)求抽取的“两位递增数”的个位数字与十位数字之积能被5整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
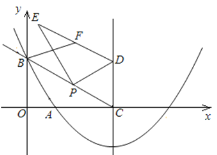
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 过点
过点![]() ,
,![]() ,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且CPD=
,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且CPD=![]() .
.
(1)求抛物线的函数表达式;
(2)若点P的横坐标为m,△PCD的面积为S,求S与m之间的函数关系式;
(3)过点P作PE⊥DP,连接DE,F为DE的中点,试求线段BF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某度假村拥有客房40间,该度假村在经营中发现每间客房日租金x(元)与每日租出的客房数(y)有如下关系:
x | 200 | 220 | 260 | 280 |
y | 40 | 35 | 25 | 20 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每日租出的客房数y(间)与每间客房的日租金x(元)之间的关系式.
(2)已知租出的每间客房每日需要清洁费80元,未租出的每间客房每日需要清洁费40元.含x(x≥200)的代数式填表:
租出的客房数 | ______ | 未租出的客房数 | ______ |
租出的每间客房的日收益 | ______ | 所有未租出的客房每日的清洁费 | ______ |
(3)若你是该度假村的老板,你会将每间客房的日租金定为多少元,才能使度假村获得最大日收益?最大日收益是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com